如何证明π是无理数
一.前言
UP只是一名初三学生,本专栏中的证明方式具体可见BV1Db411b7UL。同时因为UP第一次写这么严谨的话题和专栏,所以暂时不知道如何打数学符号,所以在一些地方会使用手写,望见谅,也希望有大佬能教UP。
二.证明方法
对于证明π是无理数我们采取反证法。假设π=u/v(其中u、v∈Z且u>v>0)。紧接着通过某种方法找出在这个假设下的矛盾以证明假设错误,即原命题正确。
三.具体思路
根据视频
BV1Db411b7UL的思维。首先我们要构造一个数列{An}(别问为什么不用I,感觉有点像1),其中第一项从A0开始。这个数列有以下两个特点:
1.对于任意的非负整数n,An为正整数。
2.当n→+∞时,An→0。(特征见下图)
从此处我们便可以轻易发现矛盾-一个每一项都是正整数的数列极限怎麼可能是0!因此,原命题得到证明。

三、证明特征
综上所述,我们的证明思路已经明确。现在便是如何证明这两条特征的问题。首先我们先写出这个数列An(如下)
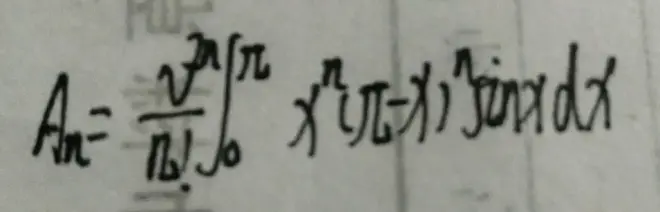
首先我们先证明第二条特征:
当n→+∞时,An→0。
在此我使用我的理解去证明这条。假设有一个函数ψ(x)=f(x)g(x)h(x),同时当x∈(a,b)时f(x)、g(x)、h(x)均大于0。并且f(x)、g(x)、h(x)在x∈(a,b)时均有各自的极大值点A、B、C。首先将ψ(x)在区间(α,b)的积分展开(如下)

注意后边,这三个函数分别的值肯定分别小于A、B、C。所以它们的乘积肯定小于等于ABC。故对三个函数值乘积的求和自然小于等于对ABC的求和(见下图)。

所以原积分的结果便小于其中三个函数的最大值的乘积乘以(b-a)。 回到原积分,当x∈(0,π)时。x^n最大值为π^n,(π-x)^n最大值为π^n,sinx最大值为1,b-a=π。又因为三个函数均非常数函数,故原积分小于π^(2n+1)。因此我们可以得出以下结果

令n→+∞,可得到下面结论。

对n!使用斯特林公式,可以得到下面结论

因此便证明:
当n→+∞时,An→0
四、继续证明
对于第一条特征我们分为两点证据
1.证明对于任意的非负整数n,An>0
2.证明对于任意的非负整数n,An为正整数
第一条很容易得证:由于y=x^n,y=(π-x)^n,y=sinx当x∈(0,π)时均大于0,故整体的函数图像必然在x轴上(如下图),故它们在(0,π)上的积分必大于0,故An>0,得证。


对于第二条我们的证明相对困难。首先,我们先计算一下当n=0、1时是否为正整数(如下)

很明显,当n=0、1时An均为正整数。那么对于任意的整数n>1,是否也存在这个结论?显而易见的是如果直接计算这个积分,那工作量会大的离谱。所以我们换一个思路,A2与A0、A1是否存在关系?An是否与A(n-1)以及后面几项相关?是否存在An的递推公式?这里我们便来尝试计算这个积分。计算方法自然是选择分部积分法。注意到sinx的不定积分为-cosx,再积分一次便是-sinx。所以理论上计算两次便可以得到递推公式。而y=x^n(π-x)^n的一阶导、二阶导也可以轻松求出。有了理论支持,我们便可以上手了。
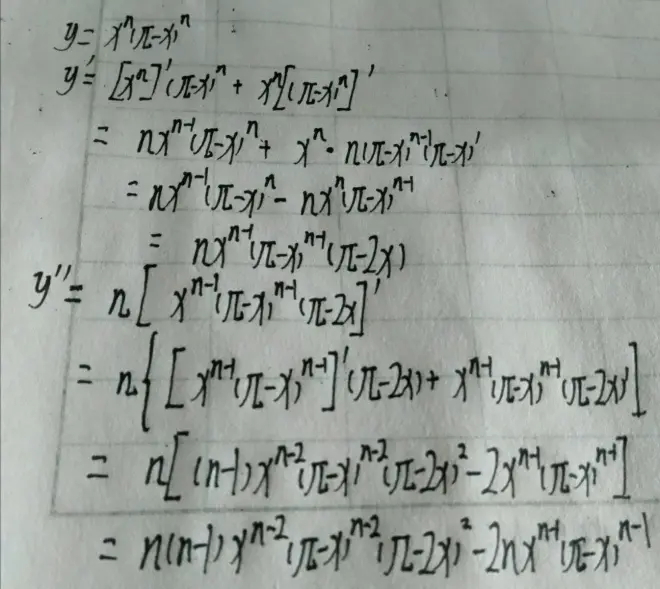
(函数的求导)
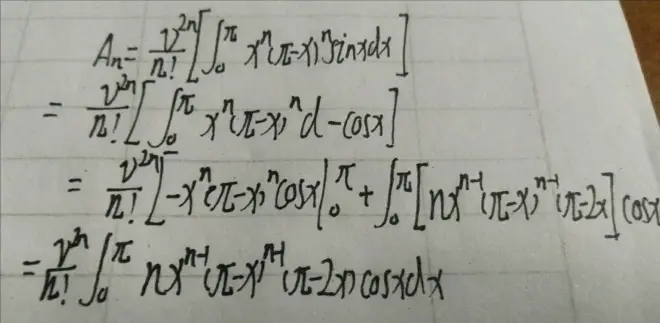
(第一次分部积分)

经过亿系列复杂的计算后,我们得到了An的递推式。很明显,2v^(2n-1)、v^2u^2均为正整数。而A0、A1又是正整数,因此A2、A了……An均为正整数。因此,原数列的两条特征被证明,原命题自然解决。
我们用严谨的方法证明出了π为无理数!
五、结言
有一说一,这个专栏的质量很低。可惜UP没有电脑,不能使用LaTeX以提高观感,只能使用这种手写的方法,希望各位见谅。同时UP写这个专栏的目的主要是防止我忘记这些知识(施佩尔乐),以后每周可能都会发一个专栏用来记叙我去年学习的奇怪的数学知识。希望各位观众老爷可以提出批评建议,当然也希望可以支持UP!

