初中数学几何模型48讲（6-12）

模型六  8字模型 (三角形五大模型）

[结论] 如图,AC与BD相交于点0，则∠A+ ∠B= ∠C+∠D

口诀:见8字，除对顶,剩余两角之和会相等.

模型七  飞镖型 (燕尾型）

[结论]如图所示,已知四边形ABDC，则∠BDC= ∠A+∠B+∠C.

口诀:见飞镖，四个角,三角之和等于最大角.

模型八  A字模型

[结论]如图所示，∠DAE的两边上各有一点B,C,连接BC，则∠DBC+∠ECB=180°+∠A。

口诀:见A字,要想角，两外之和等于顶加180°

模型九  鸡爪模型

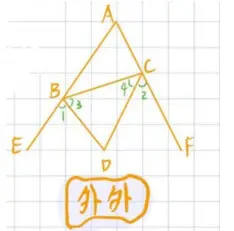
[结论] 如图所示，∠A+∠BFC=∠DBF+∠FCE

口决:腋下两角和等于上下两角和

模型十  双角平分线模型  （3个结论）

[结论1]如图所示,在△ABC中,BD、CD分别是∠ABC和∠ACB的平分线则∠BDC=90°+1/2∠A.

[结论2]如图所示，△ABC的外角平分线BD和CD相交于点D,则∠BDC=90°-1/2∠A

[结论3] 如图所示，△ABC的内角平分线B和外角平分线CD相交于点D.则∠D=1/2∠A。

口诀:内内90°加-半，外外90°减-半,内外就-半

模型十一  一线三垂直模型 （K型）

[结论1] 如图所示，AB⊥BC，AB=BC，AD⊥DE，CE⊥DE，则△ABD≌△BCE，DE=AD+CE。

口诀:手臂问距 二长手+短手  ED=AD+CE

[变式]如图所示，AB⊥BC，AB=BC，AD⊥DE，CE⊥DE，则△ABD≌△BCE，DE=AD- CE

口诀:手臂间距二长手-短手 即DE=AD-CE

 模型十二  手拉手模型  

两个顶角相等的等腰三角形，顶点重合，左底角与左底角相连，右底角与右底角相连构成的图形

[结论] 如图所示，AB=AC，AD=AE，∠BAC=∠DAE，则

(1) △ABD≌ACE

(2) BD和和CE的夹角∠BFE=∠BAC=∠D

编辑搜图

编辑搜图

[变式1]如图所示，等边△ABC与等边△CDE，则△BCD≌△ACE,∠BFA=60°

编辑搜图

手拉手，有全等 夹角=旋转角

编辑搜图

[变式2] 如图所示，等腰Rt△ABC和等腰Rt△CDE，则BCD≌ACE,∠BFA=90°

同理,SAS证全等旋转性质证夹角∠BFA等于旋转角∠BCA.即∠BFA=90°