平面三角形单元有限元程序设计（python）

2023-06-21 18:27 作者:DJ2354 0人读过 | 我要投稿

本文档为有限元方法课程作业，使用python编写，可实现任意单元数量的结构计算。鉴于搜索到这篇文章的一般都是选了这门课的同学，所以基础知识不多说直接开始：

1 程序设计

1.1 设计思路

有限元程序的基本功能为输入结构的几何信息、材料参数、荷载和约束情况，输出节点位移、单元应力应变等结果。程序采用python语言编写，二维数据和一维数据均使用mumpy矩阵存放。

（1）生成结构刚度矩阵

结构刚度矩阵是有限元计算的核心。可以使用循环结构，依次生成各单元的单元刚度矩阵并添加到结构刚度矩阵中，每次循环生成一个单元刚度矩阵并立即添加到结构刚度矩阵中，下一次循环时不保留上一个单元的单元刚度矩阵，以节约内存。为节省时间，程序中的单元刚度矩阵直接按式 1生成：

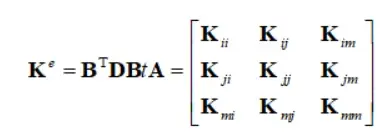
分块矩阵表示为：

其中：

（2）生成荷载向量

荷载向量可由输入的荷载信息矩阵直接生成，维度为2n，n为节点数。

（3）处理边界条件

采用对角元素置1法，将刚度矩阵中与被固定节点对应的对角元素置1，该行和列其余元素置0，同时将荷载向量对应元素置0。可在子程序中申明全局变量，直接修改刚度矩阵和荷载向量。

（4）求解大型稀疏矩阵方程

整体刚度矩阵是一个大型带状矩阵，对于这类矩阵产生的大型稀疏矩阵方程，可以调用scipy库中的sparse.linalg.spsolve函数求解。

（5）求单元应变

根据得到的节点位移，可由式 4~式5得到单元应变εx,εy,γxy。用循环结构循环计算单元应变并存入应变信息矩阵输出。

（6）求单元应力

根据得到的节点位移，可由式6~式7得到单力σx,σy,τxy。用循环结构循环计算单元应力并存入应力信息矩阵输出。

式6

式7

（6）输出结果

输出结果包括节点位移、单元应变和单元应力。

1.2 程序展示

（1）主要变量

EL：弹性模量

PO：泊松比

TK：厚度

NODE_SUM：节点数目

ELE_SUM：单元数目

NODE：节点坐标矩阵，每行为节点坐标，列按节点号排列

ELE：单元节点号矩阵，每行为单元的三个节点号，列按单元号排列，单元内节点号逆时针排列

P_inp：荷载信息矩阵，第一列为荷载作用的节点号，第二列为x方向荷载，第三列为y方向荷载

BC：约束信息矩阵，第一列为节点号，二~三列分别为x和y向的约束情况，1为固定，0为自由

TYPE：平面问题类型，1为平面应变问题，否则为平面应力问题

（2）子函数

create_K( EL, PO, TK, NODE_SUM,ELE_SUM, NODE, ELE):生成整体刚度矩阵

create_P(P_inp,NODE_SUM):由输入的节点荷载信息生成荷载向量P

do_BC(BC):处理边界条件，置1法对角元素

solve_Uout(U,NODE_SUM):根据位移向量得到节点位移信息矩阵

solve_B(U,NODE,ELE,ELE_SUM):根据位移向量U得到结构应变信息矩阵

solve_S(U, NODE, ELE, ELE_SUM, EL, PO):根据位移向量U得到结构应力信息矩阵

有限元程序完整代码如下：

2 算例验证

建立有限元算例如图 1所示。本文所有数值均使用国际单位制，即长度：m；时间：s，力：N，应力：Pa。后续数值出现时不带单位。

图1 有限元算例结构

本代码不包含前处理部分，通过更改主程序中第一部分关键参数的形式输入参数，按照注释行要求输入关键参数即可实现任意单元数量结构的计算。弹性模量设置为20，泊松比为0.2。以2点为坐标原点，1号单元长直角边为x轴，短直角边为y轴，约束1，2点x向和y向位移。荷载数值为1，作用于5号节点，方向竖直向下。主程序第一部分输入参数为：

程序运行后会在当前文件夹产生一个名为“result.txt”的结果文本，文本内容如下：