在日常工作中，我们常常收到来自JMP用户朋友的各种提问，比如：

在寿命分布散点图中，上半部分的黑点是什么？
当我研究产品可用寿命时，研究结束前产品没出现失效，该怎么分析？
研究期间记录数据，是否需要确定失效和未出现失效数量的比重？
……

其实这些问题都与删失数据相关。我们在做生存分析时，由于各种原因，用于分析的数据很可能在某种程度上被截断（比如研究时长、量具量程限制等等），导致实验对象的状态丢失，从而使我们无法获得所观测事件的精确发生时间，就产生了删失。

那么，什么是删失？它会在哪些情况下出现？发生了删失，该怎样应对？如果不小心了忽略了删失数据，会发生什么？针对以上大家关心的种种问题，我们就来一次性讲讲删失数据分析。

本文将会围绕以下5个问题来介绍删失，以及当出现删失时如何使用JMP应对删失数据。

• 什么是删失？

• 删失数据什么情况下会出现？

• 怎么“告诉”JMP数据的删失信息？

• 如果用户忽略删失数据会发生什么？

• 检测限制和广义回归模型中的左删失数据
  

01什么是删失？

在观察或实验中，由于某种原因未能观察到失效事件发生的情况下，所获得的数据（比如我们不可能无限期的观测下去，但产品始终未失效）称为删失数据。

删失数据通常分为：

• 右删失(right censored)：在预先指定的时间T，测试停止，确切寿命未知，但至少大于T；

• 左删失(left censored)：在预先指定的时间T，测试停止，确切寿命未知，但至少小于T；

• 区间删失(interval censored)：含上下边界的失效单元数据。

删失数据是可靠性分析特有的数据类型，并且其包含价值信息不可被忽略，否则将导致可靠性估计偏倚。删失数据在可靠性数据分析中非常常见，有很多种可能发生的删失情况，且这些情况有可能会同时存在：

01 时间删失（Type I）：最常见，研究过程在所有失效数据出现前就已经结束了；

02 失效数量删失（Type 2）：研究在获取到一定数量的失效数据后就停止了；

03 区间删失：已知个体在当前时间点未失效，但在未来某时间点前会发生失效。问题是我们不确定该个体在这个时间范围内哪一个具体时间点失效，但至少我们可以用这个区间限制失效发生的范围；

04 随机右侧删失：某些产品失效是由多种原因造成发生在竞争成本，我们关心某类特定的失效原因，但我们无法测量得到这种特定类型的失效发生情况，因为受到其他事件影响；

05 系统性多重删失：某些失效次数超过运行次数，交错入场的数据录入；

06 左删失：知道截至某时间点，删失已经发生了，但不知道真实的删失具体发生在这个时间点前的何时。

02 JMP中的删失类别

右删失应该是最常出现的一种删失类型，代表在研究结束前，我们关注的失效事件没有足够的时间全部发生。

常见的右删失如：

• 可靠性测验：一个产品（比如灯泡）可以持续运行多长时间；

• 生存模型：零件在研究结束前一直运作，没有失效。
   

在JMP中我们有两种表达右删失的数据形式：

• 方式1：研究单元的存活时间为一列（图中的“时间周期”），删失状态为一列，可以通过JMP寿命分布UI界面的“删失代码”功能选择代表删失的标签；

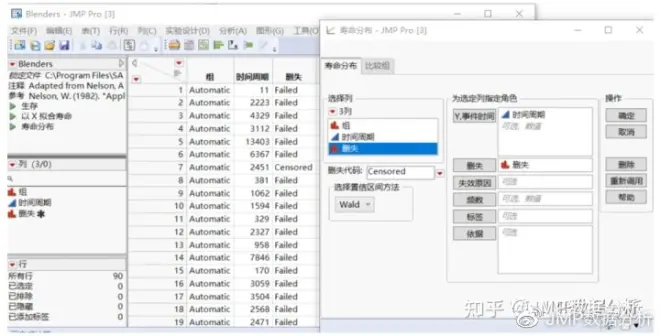
方式2：明确开始、结束时间和对应计数，JMP将据此判断删失。

左删失：关注的事件在研究和观察之前就已经开始了。

常见的情况有：首次进行检测时，失效就已经发生：

• 即正式观测开始前，单元就已经发生失效；

• 检测限制（LOD: Limit of Detection），后面的案列分享中会提到。

区间删失：区间删失是失效发生于两次观测之间，例如非连续型观测的周期性检查。在JMP中需要运用两列格式来定义区间删失（见图2的使用两列定义删失）。

 

其他

• 寿命分布-不同失效原因对应不同的删失情况

• 可靠性预测平台中的内华达形式数据

• 破坏性退化：针对非基于时间的响应

• 可靠性增长和复发分析中的Type II删失（失效数据删失）

03 JMP中的混合删失

实际研究中，除了上述各种删失出现，还有可能多种删失类型同时出现，形成混合删失情况。

如下图，JMP中用两列数据来表示。通过JMP菜单“分析”->“可靠性和生存”-> “寿命分布”-> “事件图”可以将删失具体情况展示出来：黑色点为失效单元，箭头指示删失（右删失箭头朝右，左删失箭头朝左，区间删失表现为两个箭头）。

 

04 简单统计背景知识补充：CDFs、PDFs、最大似然估计MLE

在介绍案例前，这里不得不穿插一些统计背景知识（如果对概率论和最大似然估计比较熟悉的朋友可以跳过这部分，可直接参考下一期的案例讲解）。

为了估计出后续拟合所得分布中的关键参数，我们会用到最大似然估计法。要解释最大似然估计，我们先从基础的CDF和PDF谈起：

1 累计分布函数(CDF：Cumulative Distribution Function)：一个随机变量（对应到我们的场景，其实就是可靠性数据中的事件时间）小于或等于某个值的概率：

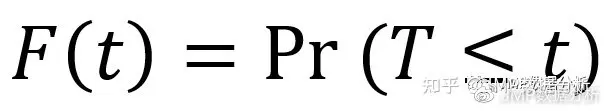
2 对于连续型分布，概率密度函数f(x) (PDF: Probability Density Function)是CDF的导数，即CDF是PDF的积分：

考虑到CDF和PDF的特性，另一种更直观的理解方式是：CDF是PDF曲线下的面积，PDF曲线下全面积之和为1.

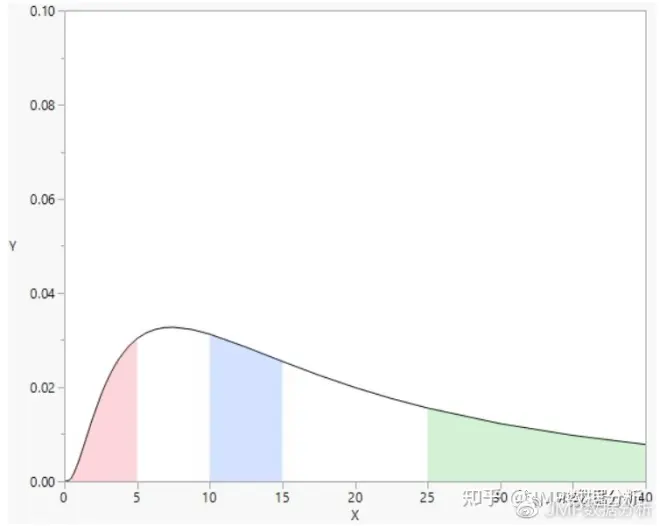
例如，下图是一个对数正态分布的PDF，其特征也非常明显：当X>0时，概率Y才是正数，即：

阴影面积：

 3 可能性/似然(Likelihood)：数据中所有观测事件发生情况都考虑在内时，其实就是计算他们的PDF乘积，即数据的联合分布(joint distribution)。

我们把这个联合分布的概率称为似然函数，它展示了当给定参数值为θ时，我们所关注的事件都发生的概率：

而MLE其实就是在给定观察数据的前提下，找到能使所有数据产生的输出值概率积（即上述的似然）最大化的参数：

• 使可能性最大的参数叫做最大似然(MLE: Maximum Likelihood Estimator)

• 因为他们使数据的联合分布概率最大化，所以他们其实最可能发生

MLEs写为：

这里μ是位置参数，σ是尺度参数。这时，删失数据情况下的MLEs就可以写为：

最大似然函数转为求区间删失上下限（u: upper, l: lower）范围内的CDF。

左/右删失数据其实是区间删失的特殊情况，即：

• 左删失：tl=0，即F(tl)=Pr⁡(T≤0)=0，即:

• 右删失：tu=∞，即F(tu)=Pr⁡(t≤∞)=F(∞)=1

有上述公式铺垫，我们就可以通过CDF和曲线下面积的形式表示删失数据，例如：

• 红色区域左删失： F(5)

• 蓝色区域区间删失：F(15)-F(10)

• 绿色区域右删失：1-F(25)

• 似然Likelihood：F(5)×(F(15)-F(10))×(1-F(25))

今天先为大家介绍了删失数据的基础，包括常见的删失数据类型，JMP中如何识别删失数据，以及对删失数据原理的简单介绍。希望可以为可靠性与生存分析相关研究领域的朋友们提供参考。我们将在下一期通过两个案例继续为大家介绍当删失发生后该如何应对。敬请期待！

想要在JMP中跟着案例实战操作的话，欢迎下载最新版的 JMP 17 免费试用。（复制链接到PC端浏览器免费下载）

https://www.jmp.com/zh_cn/download-jmp-free-trial.html?utm_campaign=td7013Z000002DxWTQA0&utm_source=wechat&utm_medium=social