高分子科学系 李卫华:神奇的嵌段共聚物自组装邂逅美妙的自洽场理论



通常焓都是正的,是不利于混合的;而熵,特别是平动熵,是有利于混合的。
如果吉布斯自由能是负的,那么说明能够均匀地混合。
如果将红色的分子和蓝色的分子各自连接起来,会导致熵的下降,造成整体吉布斯自由能的提升,从而导致宏观相分离。
这就是为什么聚合物虽然都是有机的,但仍然倾向于不混合或不均匀混合,特别是在温度降低的时候。

但是在做材料的时候,我们不希望材料不均匀混合,因为我们想利用不同材料之间互补的化学物理性质。要分布均匀才能得到宏观均匀的材料。
化学家通过利用共价键将不同的材料分子连接在一起,虽然这种新型分子不会在宏观上产生相分离,但是会在微观层面产生相分离。,这类物质就是嵌段共聚物。

为了理论上的简化,我们把嵌段共聚物的不同组成部分称为A和B。
为了研究嵌段共聚物,我们需要知道哪些参数呢?
首先,我们需要知道嵌段A所占的体积分数f;
其次,前面提到嵌段共聚物产生微观相分离的主要原因是物理化学性质上的不相容性,这种不相容性的程度就决定了产生相分离的难易程度。这个不相容性有个参数χ,称为Flory Huggins参数。此外,我们刚刚提到为什么聚合物容易不相容?因为它们的分子量变大了,自由度下降了,所以我们需要把自由度这个概念给考虑进来,这里我们叫它为聚合度N。我们把Flory Huggins参数和聚合度乘在一起,把它们当作一个参数,来描述聚合物的不相容性。
在描述最简单的二嵌段共聚物时,只需要知道f和χN两个参数就可以了。
嵌段共聚物起始很容易理解,我们可以把嵌段共聚物看成是一个圆柱。这个圆柱为了减少红色和蓝色的接触,那么它变得越细长越好。但同时,我们可以把聚合物看成是一个弹簧,这个弹簧拉伸得越厉害,它的弹性能是要上升的,这就是我们所谓的熵弹性。对于熵弹性来说,它不希望被拉伸,它希望形成随机的线条,而对于不相容性来说,拉伸得越厉害越好,所以这个因素的共同竞争才能导致一个相变,所以它就有一个最好的平衡状态,让这个聚合物达到自由能最小。

这就是二嵌段共聚物的相图,与传统的相图不太一样,常见的相图是气液固三相,横纵座标是压强和温度。而对于二嵌段共聚物的相图来说,它的横纵座标是体积分数f和不相容性χN。这个相图和气液固相图是有区别的,在严格的意义上,可能这个不能称之为相图。在气液固相图中,虽然压强和温度不同,但是代表的分子还是一样的。但是在这个相图中,f不一样,所代表的嵌段共聚物分子是不同的。在这个相图中,我们只要知道f和χN,那么就能知道这个嵌段共聚物能形成什么样的稳态结构。
这个相图是怎样建立的?这就要提到我们后面要讲的自洽场理论。自洽场理论能够计算每一种结构的自由能,你只要比较自由能,自由能低的,那么就是稳态。通过对自由能的比较,就能确定相边界。这就是我们构建相图的过程。相图对于我们实验来说,很重要。现在我们有了这个相图,想要得到哪一种结构,我们只要合成相应的嵌段共聚物就够了,而不需要通过试错的办法。我们通过理论去确定这个相图,也可以通过实验来确定,但是实验是没有办法确定这个结构是稳态还是亚稳态的,实验上是可以看到亚稳态的,只是说概率比较低一些,而且实验的时间会长很多。

自洽场理论并不难,是一个工具,都能学会。我们已经开发了一个非常好用的软件TOPS。

化学家们能够合成各种嵌段共聚物,再利用自洽场理论来计算相图,可以发无数文章,真的有这样的好事吗?

根据早期研究表明,不同的AB型嵌段共聚物所形成的相图非常相似,没有新颖的结果,不值得发文章。
现在我们从相图中可以总结,比如球状相,通常形成的是体心立方结构(BCC),其实我们平常最常见的硬球排列并不是体心立方,体心立方在金属中较为常见,当然金属中也有面心立方和六角密堆,但是嵌段共聚物为什么形成的是体心立方?这个后面我们会讲。另外柱状相是六角排列(Hexagonal Cylinders),我们很好理解,平时我们把树或管子排列起来,也是六角排列。接下来是双连续网络(Double Gyroid),它是一个三分叉的双连续网络,那么为什么嵌段共聚物不能形成其他类型的双连续网络?
在2000年以前,大家都认为AB型的嵌段共聚物只能形成这些结构。

能不能通过设计特定的分子结构来获得相应的性质?而不是合成了某种分子之后去研究它的性质。通过性质来反推分子结构和凝聚态结构是不是更加符合我们材料设计的要求?

2010年Science上发表的一篇论文,做得非常漂亮。它将PI-PLA从70度退火到40度,观察到典型的体心立方结构(BCC),这个并不奇怪,如果只是到此为止,它也发不了Science。

接着,他将PI-PLA从120度退火到25度(室温),观察到不一样的现象,接着延长退火时间到26天,观察到与BCC完全不一样的峰值。结果发现这个相是非常复杂的Frank-Kasper σ相。Frank-Kasper σ相是在距离当时50多年前在合金体系内被发现的。合金就是把不同的金属原子混合在一起形成晶体结构,因为原子的尺寸大小不一样,所以它们可以排列成很多复杂的晶格结构,其中Frank-Kasper就是其中一类复杂的晶格结构。在嵌段共聚物体系中,它是大小和形状都不相同的,那它为什么要排列成这么复杂的晶格呢?

球的排列是一个非常古老的问题,我们最熟知的就是硬球排列,一定是密堆积这种。硬球不管怎么排列,它们的相互作用是不变的,都是0,所以在硬球排列的过程中是没有相互作用的变化,它只有熵的变化,所以硬球可以说是纯熵体系。
还有一个古老的问题,那就是Kelvin问题,它就是说,等尺寸的肥皂泡如何填充空间是最有效的?经过一百多年,确定这种排列是A15,不是体心立方,它跟体心立方有点相似,但是它的每个面上是2个粒子,而不是1个。它是Frank-Kasper家族中的一员。这个肥皂泡的排列完全是由泡泡之间的界面面积决定的,有限的体积内如何让界面面积最小?它是一个纯相互作用的问题,或者说是纯焓的问题。从纯熵到纯焓,其中就有既由熵决定又由焓决定的部分。嵌段共聚物的自组装既有相互作用,又有熵,所以它是两个部分的竞争。此外,我们还可以通过设计嵌段共聚物来调控这两个部分的比例,所以我们是可以实现从纯熵的六角密堆到纯焓的A15。这个过程会经历什么结构呢?

这个过程会经历体心立方和Frank-Kasper σ相。

我们进一步分析,去看这些不同的晶格。FCC也是一种六角密堆,只不过是ABCABC排列的,普通的六角密堆是ABAB排列的。FCC的配位数是12配位,它的Wigner-Seitz Cell的形状,会有一个形状因子IQ(Isoperimetric quotients)。不同的Wigner-Seitz Cell的形状,它的圆度也是不一样的,也就是偏离球的程度是不一样的。
我们可以看到,FCC偏离球的圆度是最大的,接着是BCC,σ和A15是最小的。
这个可以从配位数的角度来解释,FCC的配位数是12,BCC是12.5,A15大概是13.5,σ比A15稍微小一点,但是两者非常接近。也就是说,配位数越高,圆度也就越圆。
那么,Wigner-Seitz Cell的圆度是如何影响嵌段共聚物的排列的呢?

如果球占满整个空间,那么这个球的形状就会变成了Wigner-Seitz Cell,也就是说,球越大,变形就越严重。变形越严重,就说明了它的界面面积就越大。那么当它的体积越来越大,界面面积越来越大,它就想尽量减小这个界面面积。那么只有通过改变它的晶格排列来减小它的界面面积。
越圆的Wigner-Seitz Cell有利于减小变形,从而减小界面能。
如果界面能越来越大的时候,这些球就倾向于排列成高配位的、Wigner-Seitz Cell更圆的球状相。
接下来,我们怎么来获得这些高配位的球状相呢?我们只需要增加球的体积分数。

只要扩大球状相的相区,增大球的体积分数,那么自然而然就会排列成复杂的球状相。

因为之前实验做的是二嵌段共聚物,没有引入链的不对称性,那就是有一个参数没有考虑进来。
构象不对称ε
构象不对称导致了σ相的稳定存在。
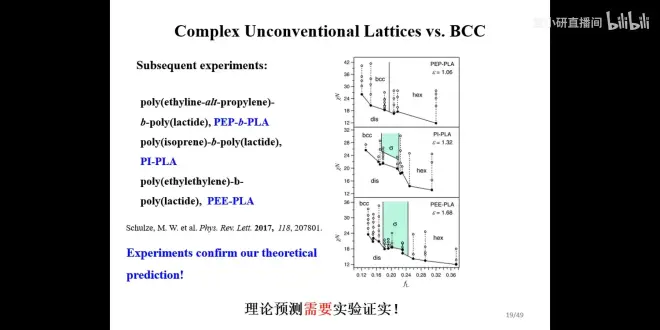
验证实验,设计了3种二嵌段共聚物,发现随着ε的增大,σ相的区域越大。






实验证实理论预测









通过减小中间嵌段的长度使晶体结构从高配位转变成低配位。



平移对称性(周期性) -> 旋转对称性(1,2,3,4,6度)
准晶体:有序但无周期性 -> 5,8,10,12度局部旋转对称性