正方形ABCD和等腰直角三角形CDE，CE=8，求梯形面积是多少。

题目：
如图，正方形ABCD和等腰直角三角形CDE组成一个直角梯形，已知CE=8，求梯形面积是多少。

粉丝解法1：
连接BC，BC=EC，将△ABC以B点为原点下转使 BA与BD重合，C点落在CD的延长线交于F点，连接FE，则CBFE为边长为8cm的正方形，梯形的面积占它面积的3/4。所以，梯形面积=8x8x3/4=48平方厘米

粉丝解法2：
S梯=3×8²/4=48

粉丝解法3：
从图中及数据，可以确定CD＝4√2
则梯形的上底＝4√2，下底＝8√2
高＝4√2，
所以梯形面积＝4√2*6√2＝48

粉丝解法4：
8*6=48
等量分割

粉丝解法5：
如图由题意做辅助线，可知△BCE为直角等腰三角形，另三个小三角形全等。所以△BCE=8x8÷2=32，梯形面积32÷2x3=48

粉丝解法6：

粉丝解法7：
如图：S阴=S正方形×3/4
=8×8×3/4=48

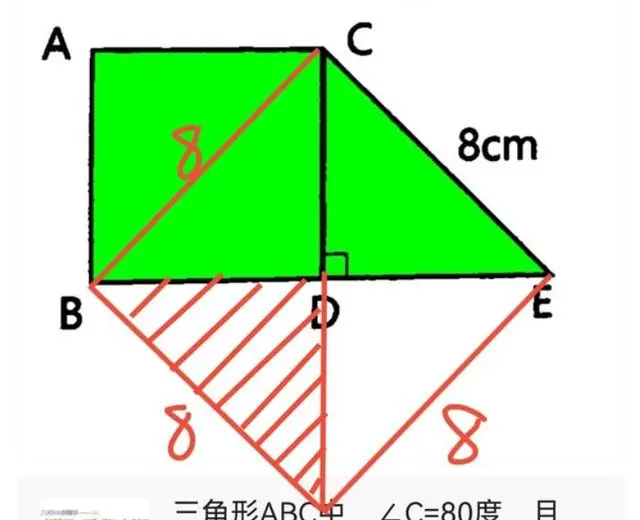
粉丝解法8：
简单点，连接BC，S△BCE=8*8/2=32
S△ABC=32/2=16
S梯形=32+16=48

粉丝解法9：
等腰直角三角形面积是斜边平方的1/4，正方形面积=2ⅹ等腰直角三角形面积，梯形面积=8x8÷4x3=48