数据结构与算法_平衡二叉树

（1）树高和性能的关系

二叉查找树的查找，插入，删除的时间复杂度为O(logn),但这是在期望的情况下。最好的情况和最坏情况差别较大。

（2）理想平衡和适度平衡

首先分析在最好的情况下，每次一分为二，左右子树的结点数均为n/2, 左右子树的高度也一样，也就是说如果把左右子树放到天平上，是平衡的，如下图所示：

在理想状态下，数的高度为logn,左右子树的高度一样，称为理想平衡，但是理想平衡需要大量时间调整平衡以维护其严格的平衡性。

那么可以适度放松平衡的标准，大致平衡就可以了，称为适度平衡。

平衡二叉查找树（Balanced Binary Search Tree,BBST），简称平衡二叉树，由前苏联数学家Adelson-Velskii 和Landis提出，所以又称为AVL树。

平衡二叉树或者为空树，或者为具有以下性质的平衡二叉树：

1）左右子树高度差的绝对值不超过1；

2）左右子树也是平衡二叉树；

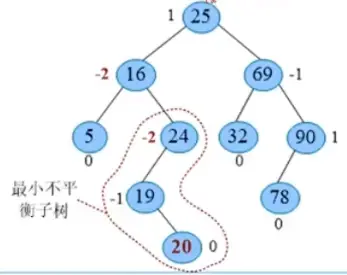
结点为左右子树的高度之差称为平衡因子。二叉查找树中，每一个结点的平衡因子绝对值不超过1即为二叉树。例如，一个平衡二叉树及其平衡因子，如下图所示：

那么在这颗平衡二叉树中插入20，结果会怎么样？如下图所示。插入20后，从该叶子到树根路径上的所有结点，平衡因子都有可能改变，出现不平衡，有可能有多个结点平衡因子绝对值超过1。从新插入结点向上，找距离新插入结点最近的不平衡结点，以该结点为根的子树称为最小不平衡子树。只需要将最小不平衡子树调整为二叉树即可，其他结点不变。

平衡二叉树除了适度平衡性还有局部性：

1）单次插入，删除后，至多有O(1)处出现不平衡；

2）总可以在O(logn)时间内，使这O(1)处不平衡重新调整为平衡。

平衡二叉树在动态修改后出现的不平衡，只需要局部（最小不平衡树）调平衡即可，不需要整棵树调整。

那么如何局部调平衡呢？

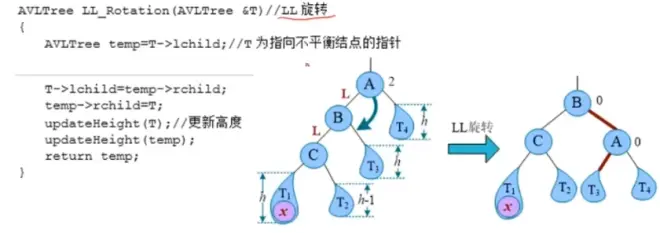
 调整平衡的方法：以插入操作为例，调整平衡可以分为四种情况：LL型，RR型，LR型，RL型。（L和R分别代表左右子树）

补：判断不平衡类型时，沿着高度大的子树走

每次旋转总有一个子树被抛弃，一个指针空闲，它们正好配对。旋转之后，是否平衡呢？旋转之后，A,B两个结点的左右子树高度之差均为0，满足平衡条件，C的左右子树未变，仍然平衡。代码实现：

代码实现：

代码实现：

代码实现：

1.平衡二叉树的插入

在平衡二叉树上插入新的数据元素x，首先查找其插入位置，查找过程中，用p指针记录当前结点，f指针记录p的双亲，其算法描述如下。

算法步骤：

1）在平衡二叉树查找x，如果查找成功，则什么也不做，返回p；如果查找失败，则执行插入操作。

2) 创建一个新结点p存储x,该结点的双亲为f,高度为1。

3）从新结点之父f出发，向上寻找最近的不平衡结点。逐层检查各代祖先结点，，如果平衡，则更新其高度，继续向上寻找；如果不平衡，则判断失衡类型（沿着高度大的子树判断，刚插入新结点的子树必然高度大），并作相应的调整，返回p。

2.平衡二叉树的创建

平衡二叉树的创建和二叉查找树的创建类似，只是插入操作多了调平衡而已。可以从空树开始，按照输入关键字的顺序依次进行插入操作，最终得到一颗平衡二叉树。

算法步骤：

1）初始化平衡二叉树为空，T = NULL;

2) 输入一个关键字x,将x插入到平衡二叉树T中；

3） 重复步骤2）,直到关键字输入完毕。

3.平衡树的删除

平衡二叉树的插入只需要从插入结点之父向上检查，发现不平衡立即调整，一次调平衡即可。而删除操作则需要一直从删除结点之父向上检查，发现不平衡立即调整，然后继续向上检查，检查到树根为止。

算法步骤：

1）在平衡二叉树查找x,如果查找失败，则返回；如果查找成功，则执行删除操作（同二叉查找树的删除）;

2) 从实际被删除结点之父g出发（当被删除结点有左右子树时，令其直接前驱（或直接后继）代替其位置，删除其直接前驱，实际被删结点为其直接前驱（或直接后继）），向上寻找最近的不平衡结点。逐层检查各代祖先结点，如果平衡，则更新其高度，继续向上寻找；如果不平衡，则判断失衡类型（沿着高度大的子树判断），并作相应的调整。

3）继续向上检查，一直到树根。