Differential Geometry Notes- Geodesics
最近在学 Do Carmo 的Differential Geometry 和 Carroll 的 Spacetime and Geometry(虽然后者是基于manifold讲的,但是学校教的还是古典微分几何),记录一下学习过程 ovo

1. Definition of geodesics
A curve on a surface is said to be a geodesic if the geodesic curvature
at every point of
.
Thus, a geodesic curves only because of the curving of the surface – the extent of internal curving is
zero. Here,
.
Free particles move along paths of “shortest possible distance,” or geodesics. In other words, particles try their best to move on straight lines, but in a curved spacetime there might not be any straight lines.
Light is always travelling along geodesics (null geodesics, with )
2. Velocity and accleration vectors
Suppose there exists a diffeomorphism map for a regular surface S, and a regular curve
that on S , then consider the tangent vector(or velocity vector) is given by:
then the accleration vector is given by:
also by chain rule we have:
and
therefore, the accleration vector by chain rule above is exactly in the form:
The formular above is very complicated, therefore we apply Einstein notation to simplify.Here, donate , obtain:
the first term indicates the linear combination of natural basis
and
in tangential space
.Then we consider the second term
.
Actually, the form of indicates the change of basis along the trajectory
. To express this change in canonical basis
, we have the following in Einstein notation :
Here, since there are 4 directions for change and each direction has 2 basis,
thus there are 8 different .The
is called Christoffel symbol, and the
for the normal component is the second fundamental form of the surface.(Revision for the second fundamental form:
)
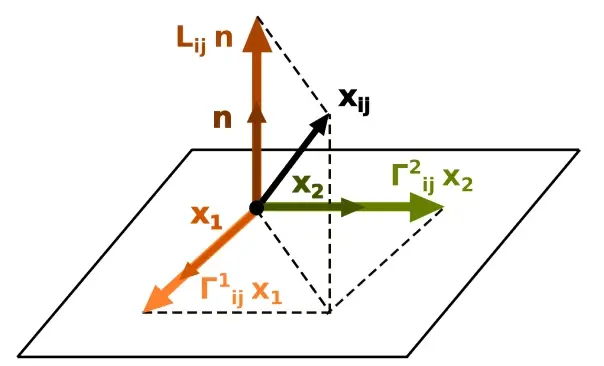
component of change of basis
Christoffel symbols describe how the direction of basis deviates from the straight line. The Christoffel symbols however, indeed describe the chage of grid of the coordinate on the surface.
3.Calculation of Christoffel symbols
3.1. Review of the first fundamental form
First, let's review the first fundamental form of regular surfaces. The 2 tangential vectors at the point on the surface are
and
, and a trajectory
.Also review the tangent vector of the trajectory at
is
.
the first fundamental form is the self inner product of the tangent vector, that is:
In tensor form, the first fundamental form is given by , which is actually the metric tensor of the surface. In
, the metric tensor is a
symmetric matrix, with:
its inverse, in Einstein notation, is expressed as , therefore
by calculation of inverse matrix, it is trivial to obtain:
3.2. Calculate Christoffel symbols
Remind that the acceleration vector is:
and noticing the geometric relationship, the normal vector is perpendicular to the tangent space
, therefore we can calculate the Christoffel symbols by doing inner product, that is:
therefore by mutipulying the inverse, we have:
or
In detail, in an orthonormal coordinate,where , we have the following:
4.Geodesics
With the arrangement above, we have the accleration vector below:
By the definition of geodesics, ,and because
we have:
because
therefore if and only if
which is the differential form of geodesics.
Expand Einstein notation, we have the following :
With orthonormal basis, the geodesics behaves:
5.Null geodesics
Back to the beginning, consider the null geodesics, in which massless particles are travelling along,like photon. Suppose a path along the ,then the metric is:
With parametrization , we have:
donate ,the null geodesics is :
With parametrization of propertime , we have:
where

