一些统计学习

2019-12-20 23:32 作者:露保协 0人读过 | 我要投稿

Formal Formulation of Statistical Learning

统计学习和传统的统计问题不太一样。传统的数理统计想要通过数据推断模型参数，统计学习想要推断的是函数。采用的数据是函数的input和output：{(x_i,y_i)}（这属于supervised learning；没有y_i属于unsupervised learning）。

"A problem of finding a desired dependence using a limited number of observations."

这个说法有点含糊其辞。我们需要formal formulation。

G是一个input的generator，可能是随机的，也可以是人为设计的。S是一个supervisor（有输出，所以是监督学习），相当于一个黑箱，或者说它就是statistical model。它根据某个条件概率F(y|x)输出随机的y。F(y|x)是我们不知道的。LM是一个learning machine。它的取值在{f_\alpha(x)}这个函数类里面，通过training data{(x_i,y_i)}decide出一个f_\alpha(x)，作为supervisor的一个近似（supervisor本身未必有一个函数形式，但是可以想办法用函数去近似它，比如后验众数等等）。

有了LM，我们有两个目的：prediction（比如预测x_0输入的输出）与inference（比如比较两个因素的效果哪个强）。

既然是要推断函数，就有两种：参数（限定函数空间）或者非参数（无穷维的函数空间上干事）。本文只考虑两种简单的参数问题，即限定为线性函数（linear regression）和indicator function（classification）。

仍然可以用传统数理统计的哲学去思考：

要一致地考虑统计模型的测度族中的所有参数；
用decision theory的角度去看。拿到数据之后，根据数据构建（decide）一个statistic （estimator/learning machine）\hat{f}（它是一个随机函数而不是随机变量了，归于更广泛的随机元的定义，所以这个statistic得打上引号），这个statistic应当与实际的f比较接近。度量接近程度，仍然可以用传统的MSE。但是现在有一个问题，statistic是随机函数，不是一个数，没法直接算MSE。我们可以考虑risk functional

来作为decision与真实值的偏差。把这个risk最小化的\alpha就是learning的“标准答案”。但是我们不知道F(x,y)，所以没法得到这个确切的标准答案（其实我们已经知道，如果是MSE的话，最优的“标准答案”就是后验均值，等等；但这是一个理想化的东西，我们只能尽量接近它）。统计学习要做的是minimizing the risk functional on the basis of empirical data。所以要在某些点上算这个随机函数的取值。这个“某些点”就会有讲究了。如果我们在training data set里面取，得到的是training MSE，它并不是我们感兴趣的，因为因为我们本来就知道这些点上面的取值，没有prediction的必要了。我们感兴趣的是test MSE，即在新的test data上函数的取值。评判一个statistical learning method的优劣，用的应该是test MSE。对于classification问题，上面的讨论用training error rate和test error rate代替即可。

跟传统统计学相比，感觉统计学习的方法都是highly practical的，并不是很在意统计模型到底咋样，不管怎样都行，直接学习就完事儿了。

一些trade-off

数理统计中出现的bias-variance trade-off现在在统计学习中有很多表现：

这些trade-off中根本性的一个是bias-variance trade-off。我们熟知MSE的分解公式：

理想的情况下，Var和bias应该同时很小，但是这一点是无法做到的。在传统的数理统计中，我们找不到一个optimal的estimator，会转而考虑一些compromise，譬如Pareto optimal的estimator，比如限定在unbiased estimator中的UMVUE。但是unbiased并不是什么非得满足的事情，虽然它看起来的确挺好，但是有时牺牲unbiasedness会换取更小的MSE。经典的例子就是Shinkage estimator。现在在统计学习中类似，var和bias按下葫芦浮起瓢：

当模型的flexibility上升（比如说自由度变多，变成更高阶的多项式模型），bias当然更小，但是随机函数\hat{f}对于数据更加敏感，所以var更大。总的trade-off的结果就是，MSE（test MSE）呈现U-shape。Flexibility过高称为过拟合，过低称为欠拟合，U-shape最低点处才是最好的拟合。

上面讨论的是test MSE。对于training MSE，当然是flexibility越高越小的，overfitting越厉害，training MSE越小。不过我们并不看training MSE，而关注test MSE。

另外一个同时存在的trade-off就是解释性的问题。如果flexibility很低，比如线性模型，那就很容易解释，比如Y受X_1和X_2哪个影响更大，看看参数就知道了。但是flexibility比较高时，上面这种解释性就削弱了。

线性回归

线性回归是所有统计模型中用得最多的。它是有明确的统计模型假定的（即supervisor的假定）：

注意同方差的假设（homoscedastic）是必要的，没有它就干不了活。一般还假设\epsilon~N(0,\sigma^2)，不过它有时候可以去掉（对于Gauss-Markov定理）。

Learning machine想干的就是estimate \beta_0,\beta_1,\sigma^2。这就回到了传统的统计问题。得到估计值\hat{\beta_0},\hat{\beta_1}之后，我们怎么evaluate它们？Evaluation基于residuals:

根据residual画出的residual plot是直观观察一个regression效果的好东西：

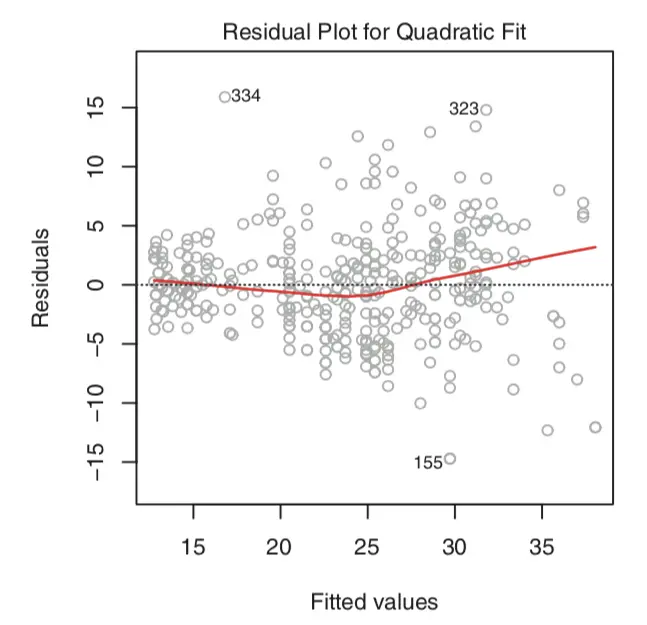
而总的拟合效果按照residual sum of squares来考察：

Gauss-Markov定理

对于前面的假设，best linear unbiased estimator (BLUE)为最小二乘估计。

Linear指的是estimator为y_i的线性组合，best指的是（在无偏的时候）var最小。

这个定理不需要对\epsilon的具体分布有任何假设。

具体来说，\beta_0和\beta_1的最小二乘估计为

记法很简单：\beta_1是关于y线性的，而且大概是y/x这个样子。\beta_0使得拟合曲线刚好过数据点的重心。

另外误差项的无偏估计为

n-2是很好理解的。方括号里面剥掉了\bar{x}和\bar{y}的两个自由度。

另外值得一提的是，Gaussian假设下这个最小二乘估计正好也是MLE。

下面给出多元的情况。多元的线性回归模型的statistical model为

Y仍然是一个数，但是X是一个行向量，\beta是一个列向量。这个表达式强调了，我们说的linear是\beta的linear，X内部包含X^2,sinX之类的都是无所谓的(所以线性回归用来拟合多项式、bsinx之类的形式完全是可以的，这点从名字来看有点误导性。但是sinbx这种就不行了)。X中通常把第一项取为常数1，表示截距。

现在我们有了training data，data仍然可以写成上面的方程：

但是此时Y是一个列向量，X是一个矩阵了。X和Y包含了所有的数据。MATLAB里做回归也是按照这种标准格式来的。

最小二乘的结果为（此时只有一个统计量\beta，所以其实比一元情况更简洁）：

它是Y的线性组合（符合BLUE）。记法：X^{-1}Y，插入两个X^T项。X本身不一定是方阵，所以Y=X\beta不是一个well-posed的线性方程问题，没法用X^{-1}Y求解。但是我们有X的Moore–Penrose广义逆(X^TX)^{-1}X^T，这就是替代X^{-1}的最小二乘解。

注意，这个写法默认了X^TX是可逆的，即X的各列是线性无关的。若不然，说明自变量中存在严格的线性关系（collinearity），此时回归问题不是良定的（三维空间中，一条线上的数据显然没法拟合出一个平面），必须剔除掉这个线性关系。

另外误差项的无偏估计为

统计量的分布

做假设检验和区间估计都需要知道上面的最小二乘统计量的分布。它们的分布总结在下面的定理中：（都是在正态假设下；直接写多元的情况，更加简洁）

其中，\beta的分布直接可以通过\beta的表达式推出来。\sigma^2的分布也是显然的。二者的独立性类比于Fisher的那个定理。（这个分布说白了就是Fisher那个定理的推广）

有了这些分布就可以做假设检验和区间估计了。比如\beta_1的1-\alpha的置信区间为

预测

现在我们想要对于input x_*的输出做出预测。不仅想要知道估计值，而且需要估计区间。

这个问题说白了就是想要估计参数\beta_0+\beta_1x_*。

为此，我们需要知道\beta_0+\beta_1x_*的分布：

从而1-\alpha的置信区间为

这样一来统计学习的两个目的：inference和prediction都完成了。

Assessing the extent to which the model fits the data

有两种办法：residual standard error与R^2。

Residual standard error就是\sigma的estimator:

它是一种lack of fit的刻画，但是问题在于它取决于Y的scale。给出一个RSE为100，你并不好判断它到底算大还是小。所以更常用的是R^2统计量。它定义为

这样理解：TSS是Y的总的variability，其中线性回归能够解释的部分是TSS-RSS，所以这个比例越大，说明能够解释的比例越大，拟合越好。

这个R^2有一些问题。它是作为

的一个estimator，但是这是一个biased的estimator。其中一部分原因在于商的期望本来就与期望的商有偏差；另一部分原因在于自由度。这个问题在multi-dimentional regression中会变得很严重。如果考虑自由度的修正，我们可以很自然地得到下面这种adjusted R^2:

这是一个less biased estimator。它一定小于原来的R^2，所以肯定小于1，不过可能会变成负数。在高维情况下，这种修正是必要的。

线性回归可能出现的若干问题

问题1:非线性性。可以从residual plot看出来：

右边没有明显的pattern，所以线性关系差不多是对的。左边有一个U型的pattern，所以需要考虑加入非线性项。

问题2:异方差性。它也可以通过residual plot看出来：

左边这种就有明显的异方差性了。我们知道Fisher-Behrens问题迄今还没解决，所以我们不指望有对于异方差性的完美的解决方案。我们能做的只是妥协：用上凸函数，比如lnY，把数据做变换，使异方差性减小。仅此而已。

问题3:outlier。指的是某个output y离预测值非常远。它也可以通过residual plot看出来：

对于outlier，如果我们知道它是误差导致的，那直接扔掉就行了。不过如果是因为模型的缺陷导致的，就要仔细考虑了。

怎么判别outlier？上面只是看着像。一个定量的判别准则是，画studentized residual plot，即除以RSE，在这样的图上，超过+-3的点概率为0.27%，可以认定大概就是outlier了。

Outlier对于估计值的影响其实不算大。比如下面这张图中，有没有去掉outlier，拟合的曲线基本没有变化。但是outlier对于区间估计影响很大。你想，一个很大的residual把estimated sigma提得很高，估计的区间就会变的异常大。

问题4：high leverage points。相对于outliers，它指的是x离得比较远的点。它对于拟合曲线的影响很大（为什么呢？后面会说）：

如何判断一个点是否属于high leverage point?我们可以用Leverage Statistic。回到最小二乘法：

红色的这个projection matrix H把Y的数据投影到拟合值（它显然是一个幂等矩阵）。这个矩阵的意义在于，h_{ij}刻画了i这个input对于第j个output的预测的影响大小。因为幂等性，

所以对角元h_{ii}就刻画了第i个input对于所有output的预测的影响的总大小，因此它称为第i个输入的leverage。所谓的high leverage指的就是这个leverage statistic比较大。

下面具体研究这个H矩阵的性质。首先，h_{ii}\geqslant h_{ii}^2，故h_{ii}\leqslant 1。其次，显然有h_{ii}\geqslant 0。接着考虑H的迹：

也就是说，平均的leverage是(p+1)/n（这里用p+1是为了把p作为predictor的数目。在X矩阵里，列数比predictor数目要多一，对应着截距）。作为一个经验法则，如果某一个input的leverage超过了平均leverage的两倍，我们就认为它可能是一个high-leverage point。

对于简单线性回归，我们可以很容易算出此时的leverage statistic为

其含义是很直观的。

这个地方需要多说一句：前面好像默认了“离其他input比较远的点，对拟合的影响比较大”。这个说法是对的，因为leverage statistic的定义完全是按照对于拟合的影响来定义的，而算出来的结果则跟这个点离其他input的距离有关。所以这个联系是存在的。

问题5:共线性。几个predictor之间的强线性关系会导致X接近于不满秩，这样虽然还是能做拟合，但是拟合的误差会很大。（可以想像，我们想要在三维空间中的若干数据点来找出一个平面，尽可能接近这些数据点。但是如果数据点位于一条直线上，就有无穷多个符合要求的平面存在，回归问题变成ill-posed。不过另一种情况是，比如说，（正的）X和X^2，虽然完全是一一对应，但是并不是线性关系，所以不会破坏回归。这就是多项式回归的道理。在三维空间中，一条曲线拟合出一个平面是可行的。）

如何检测collinearity？一个办法是看协方差矩阵。如果其中有一项很大，说明对应的两个predictor之间有较强的线性关系。但是它的局限在于，如果是三个predictor之间的线性关系，就没法检测出了。所以更好的办法是计算VIF（variance inflation factor），即某个\beta_j的方差从单变量模型道full model的扩大倍数。一个经验规则是，VIF超过5-10就指示有collinearity。

VIF有一个很直观的计算方法：

这里指的是用去掉X_j之外的所有predictor来拟合X_j得到的R^2。如果真的存在某种线性关系，这个R^2会接近于1，所以VIF会非常大。

解决collinearity的方法：1.去掉一个predictor；2.把collinear的变量结合成一个，譬如说做均值作为一个新的predictor。

MATLAB实现

以MATLAB自带的关于汽车的数据为例。我们想要获知汽车的mpg（miles per gallon）与horsepower以及weight的关系，假设这个关系的形式为mpg=a+b*horsepower+c*weight+d*horsepower*weight。

load carsmall

x1 = Weight;

x2 = Horsepower;

y = MPG;

X = [ones(size(x1)) x1 x2 x1.*x2];%注意这里是按照标准的回归格式写的

[b,bint,r,rint,stats]=regress(y,X)

scatter3(x1,x2,y,'filled')

hold on

x1fit = min(x1):100:max(x1);

x2fit = min(x2):10:max(x2);

[X1FIT,X2FIT] = meshgrid(x1fit,x2fit);

YFIT = b(1) + b(2)*X1FIT + b(3)*X2FIT + b(4)*X1FIT.*X2FIT;

mesh(X1FIT,X2FIT,YFIT)

xlabel('Weight')

ylabel('Horsepower')

zlabel('MPG')

view(50,10)

hold off

输出的结果为：

四个参数的估计值：60.71，-0.0102，-0.1882，0.0000385。
四个参数的95%置信区间[51.39,70.03]等等。
error variance的估计为15.2363354389984。
R^2为0.7742。

回归的曲面如下图所示。

分类

分类问题的formulation就是：有一个supervisor把输入（按照一定随机性）归入不同的category里面。我们希望训练出LM来模拟这个supervisor。这个LM的结果应该是input空间的一个indicator function，或者等价地说就是分类的decision boundary。

三种常用的classifier是逻辑回归，线性判别分析，以及KNN。

逻辑回归

逻辑回归是有明确的统计模型假定的（即supervisor的假定）：对于输入x，y为1的概率为e^{\beta_0+\beta_1x}/(1+e^{\beta_0+\beta_1x})，其余概率为0。然后我们的learning machine想要学习的就是\beta_0和\beta_1。学习方法用的是MLE，不过这个MLE没有解析解，都是直接用计算机数值求解的。训练完成之后，我们不仅可以做分类，而且可以具体地知道对于输入x，它有多大的概率属于第一类，多大的概率属于第二类（在模型正确的前提下）。

逻辑回归适用于多元输入以及大于两个category的分类，但是后者通常不用逻辑回归。

MATLAB中逻辑回归包含在fitglm这一广义线性回归的函数里面，用predict函数做预测。