极限手法与技巧
前言提要:本总结由学习考研竞赛凯哥相关资料与自我刷题经验总结,如有侵权,会立即下架!本文仅用于学习交流与自我记录,严禁任何形式转载与盗窃。

一、非零因子代入以及替换等价无穷小
1> 乘除里用等价无穷小
2> 加减谨慎使用无穷小(“+” 商为 -1 ,“-”商为1时不可用!)
其原理仍是泰勒,以及(x->0)低阶+高阶~低阶,但无穷小有时会导致精度不够
3> 添项、减项以凑无穷小

4> 反用无穷小

二、指数相减提取后式,构造 “e的x次方-1”
实质上就是 1~1 类极限,通常与其他方法组合使用

三、根号差使用有理化
主要用于构造平方差,一般会除以一个“+”项,而它可以用非零因子代入

四、幂指函数通常取对数
首先观察式子是不是1的无穷大,如果是,就可以用等价无穷小代换
如果不是,有必要考虑其他方法,如洛必达法则
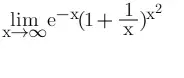
五、“∞-∞”
1> 如存在分母可以先通分,可利用(x->∞)高阶+低阶~高阶去掉其余项,留下最高次项
2>如两式变量类似,也可提取等价无穷大进行泰勒展开

六、阶的吸收律
实质是在趋向的过程中,其中一个值相对另一个值太小可忽略不计。
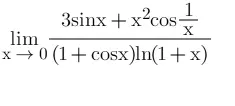
七、简单常用无穷大

lnsinx ~ lnx / xlnx = 0 可得: x ln(sinx / arcsinx / arctanx / tanx)=0

八、洛必达降阶

九、泰勒展开(最常用也是最重要的方式)
1>直接求某个泰勒展开
复合函数泰勒展开,外部函数需要展开到多少阶取决于内部函数的最低阶。但这个过程中,展开内层函数时各个函数展开都是不确定的(通常越往后越少)
2>提取等价无穷大进行泰勒展开
3>求某个复杂的等价无穷小
本质是泰勒和“低阶+高阶~低阶”的结合使用,其中最低阶即为等价无穷小
4>求参数,使无穷小的阶尽可能的高
即消除尽可能多的低阶项
5>已知极限,反求参数[需要推理过程]
6>抽象函数展开
直接使用麦克劳林公式代入。
[太累了……不想打数学公式了,不上例题了]

极限小技巧
1、和差化积
利用积化和差来记忆
在求不定积分、两函数相减的极限中有妙用!
2、乘除因子中有以下简单关系:
sinx+x~2x 类似地:tanx / arctanx / arcsinx /
使用的是低阶+高阶~低阶[无穷小]
3、等价无穷大的阶吸收律
遇到根式,可先化成顶点式,后续低次可去。[也可以一步到位,直接留下最高次]
4、极限运算法则的推广
前提条件:两者极限均存在
只要其中一项极限存在,就可以拆开
5、倒代换 t = 1/x
有时会有奇效!!
6、推广无穷小:
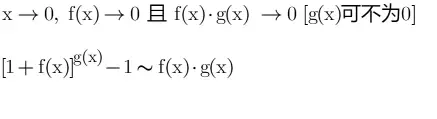

14、泰勒展开时都遵循以下规律:
奇函数只有奇次项、偶函数只有偶次项

17、tanx泰勒展开

18.学会使用lnab = lna+lnb / ln(a/b) = lna-lnb
码字不易,总结不易,如对你有帮助或者疑问的地方请及时与我联系!
欢迎讨论,但我非常厌恶自以为是的态度和怀揣恶意的想法,比如说我这举的例子都是野题(都是听课和资料上摘抄的题目)或者说是摆上来显摆的,那么对不起,我写这些也不是给你看的,哪里凉快待哪去。也不要说“卷”一词,学习就是学习,学习是正向且十分正常的事情。
Ps:如对朋友们有收获我就非常开心了,但我也不介意一杯奶茶作辛苦费~