这里是官方认证的优秀科代表渡鸦~今天是正余弦定理化简有关内容哦，如果对你有帮助请点个免费的赞吧

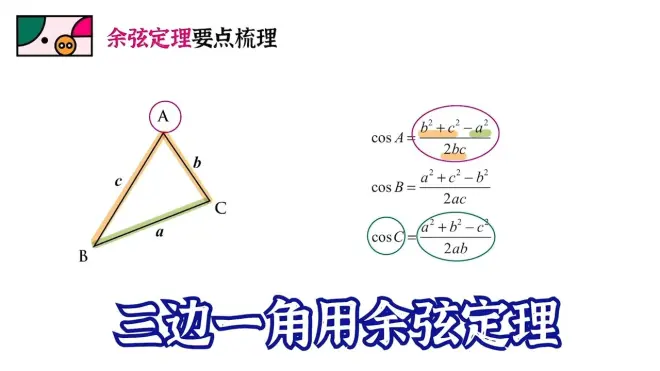
Part 1：基础公式

不多赘述，总之是有边角关系的时候用正余弦定理。

看一道小练习

转换思路有两种，边化角和角化边。本题先用正弦定理得出边长间关系，再用余弦定理求余弦值。

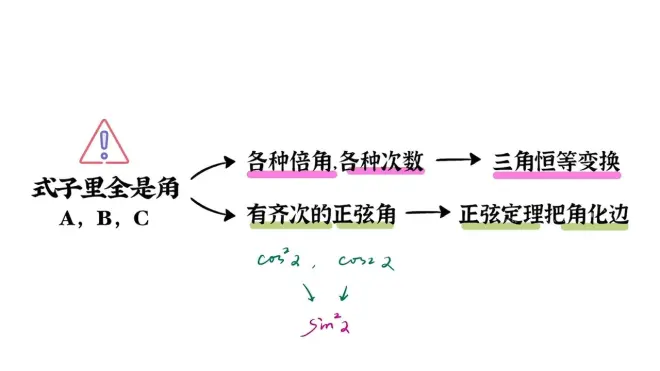
Part 2：只含角化简

这里直接给出总结

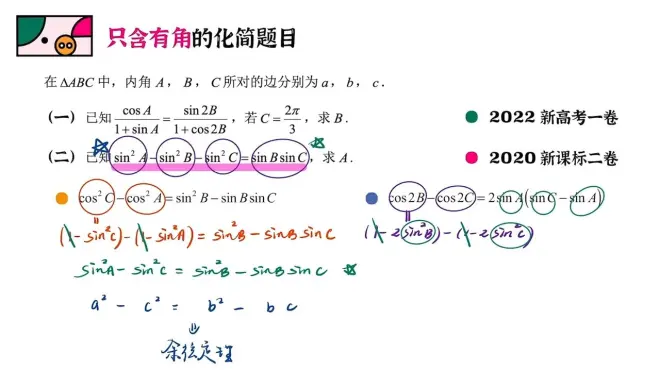
例（一）看起来还有点难度

角倍数不同，先化同角。这里角B是两倍，而A是一倍。

还是三角恒等变换的知识，升幂扩角。然后用A加B加C等于π化简。

再看例题（二）

倍数相同，全是正弦，直接化边。

发现其实就是一个余弦定理的形式，带进去整体换掉就好。

变式与（二）本质上区别不大。

存在两倍/平方余弦，化成正弦，然后化边。

目的是构造一个齐次的正弦式，方便使用正弦定理转化边。

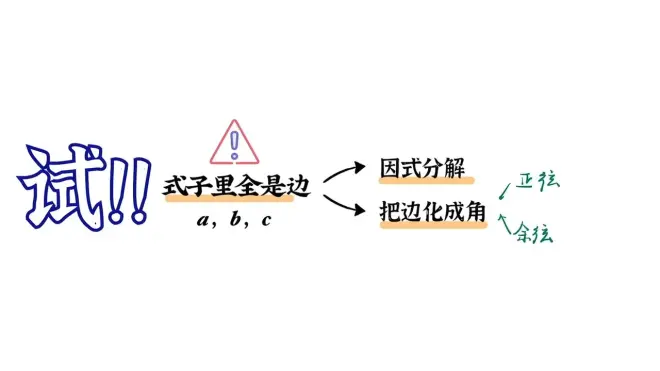
Part 3：只含有边的化简

这道例题很难

首先题目条件似乎正余弦都可。

但尝试正弦定理之后发现似乎走不通（如下图）。

这时就赶紧换成余弦了。这里有bc项所以代cosA的式子。得到2b cosA=c-b

由于刚刚是用边表示cosA，这里只能把所有的边换成sin，得到2sinBcosA=sinC-sinB。（否则又变回去了）

然后就是用A加B加C等于π去消掉一个角。具体就是：Sin C等于Sin A+B，然后再展开。

最后得到sinB=sin(A-B)。注意！不只是B=A-B，如果B+(A-B)=π也有可能，要判断这种情况。

Part 4：多条件混合化简

一句话：往条件上靠。

条件有一个2倍的B肯定要恒等变换一下的，变化完发现是cosB与边bc的关系。

那么左边的式子就应该把sinB化成cosB，然后再化边求解。

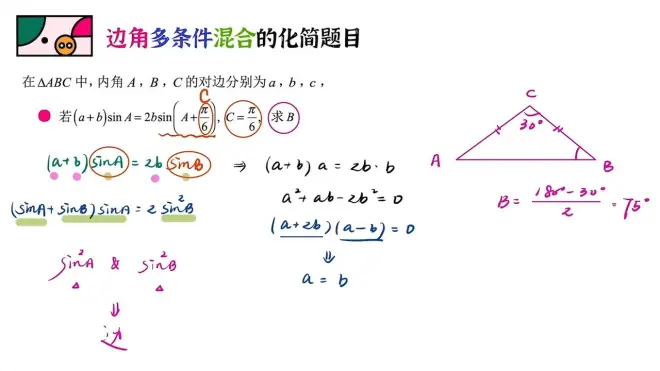
这道题等式中没有C，那只能是把六分之π换成C去写了。

还是A加B加C等于π的那个变换。sin(A+C)=sinB

接下来尝试边化角发现走不通很难化，就去角化边。这时就用到上一Part有提到过的因式分解了。

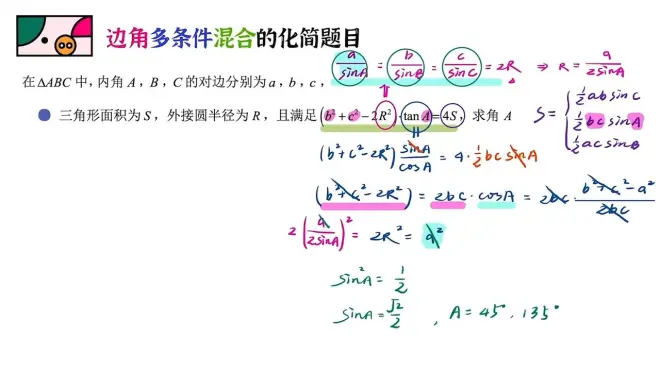
正弦定理是有一个求面积的推论的。也就是上图右上的S=0.5 a b sinC=0.5 a c sinB=0.5 b c sinA

由于左边b和c是对称的，我们自然要把S换成bc sinA来呼应左边。

这里tanA只能化成sinA/cosA，不然我们没有定理能够化简它。

这样得到b^2+c^2-2R^2=2bc cosA，肯定要用余弦角化边的。