因子模型：套利定价理论APT

套利定价理论APT(arbitrage pricing theory)由Stephen A.Ross在1976年提出。

因子的暴露系数（factor exposures）表示为，各种因子的回报表示为，那个这个股票的回报表示为：

其中表示特别回报，就是因子无法解释的那一部分回报。APT模型假设这个特别回报跟其它的因子回报或者其它股票的特别回报是不相关的。

股票的风险可以用回报的方差衡量。这个方法最先由Markowitz提出。

接下来，看一个两个因子的模型：

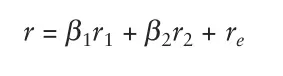
股票的风险就是股票回报的方差。

我们可以用附录中关于方差的公式求得上述式子。也可以用一个技巧，看以下式子：

只要把股票回报的平方式子中的表示为,表示为就会得到股票的方差。因为和或者都是不相关的，所以它们的协方差不会出现在股票回报的方差的式子中。

股票回报的方差也可以表示为：

简化上面这个式子，用另一种表示方法：

更进一步，把这个式子再表示成：

这个式子可以用下图形象地表示。

回到下面这个式子：

构造一个因子模型需要提供的参数包括了：

1、因子暴露系数矩阵（factor exposure matrix），记做。如果有个股票，个因子，那么这个矩阵就是一个的矩阵。

2、因子协方差矩阵（factor covariance matrix），记做。

3、特定方差矩阵（specific variance matrix），记做。如果有个股票，那么这个矩阵是一个的矩阵，其对角线上的元素即为特定方差（specific variances），又由于特定方差之间假定是不相关的，所以其非对角线上的元素为0。

附录：用到的一些公式