数电仿真4:组合逻辑电路设计
这周太浪了,下周一定好好学习。
1、用7400设计一个无弃权四人表决器,在四人或三人表决为1时通过,否则不通过。要求按组合电路设计要求写出真值表、卡诺图、逻揖函数表达式、逻辑电路图;并用实验方法验证设计结果。
要求:
(1)用2个7400(8个二输入与非门)实现最简设计;
<1>根据逻辑功能描述进行逻辑抽象,确定输入和输出变量
四个输入变量,表示四人的表决情况,记为A、B、C、D。
一个输出变量,表示表决的结果,记为Y。
<2>列出真值表,由真值表得出最小项表达式;

Y=A'BCD+AB'CD+ABC'D+ABCD'+ABCD
通过卡诺图进一步化简

得Y=ABC+ABD+ACD+BCD,即为最小项表达式
<3>选定所使用器件的类型;
7400是四-二输入端与非门,故选择与非门。
<4>根据器件的逻辑功能,化简或变换最小项表达式;

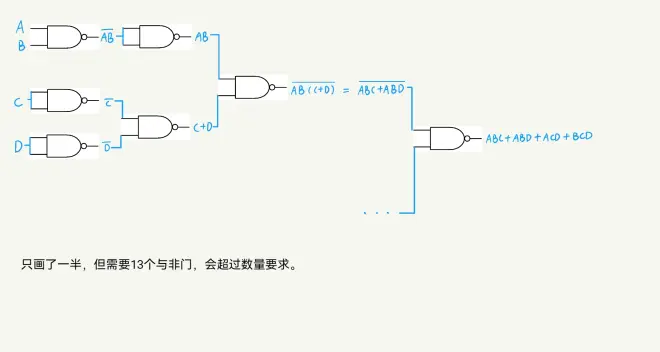

根据电路图写逻辑式Y=((((BC)'(BD)')'A)'(((AD)'(BD)')'C)')'
(第一步分成两部分的方法不唯一,所以电路、化简得的逻辑式也不唯一)
<5>根据化简变换后的逻辑表达式画出逻辑电路连接图。

通过逻辑变换器验证√

(2)改善设计电路,使对称性完好,无竞争冒险现象。(选作)
第一层的输入都经过了0个门,第二层的输入都经过了1个门,第四层的输入都经过了3个门,而第三层的输入有有经过0个门,有经过2个门,需要统一,故做如下修改

这样第三层都经过了2个门,对称性完好。
2、用与非门7400和异或门7486实现一位全减器。
<1>根据逻辑功能描述进行逻辑抽象,确定输入和输出变量
输入:减数A,被减数B,被借位Bin
输出:差D,向高位借位Bout
<2>列出真值表,由真值表得出最小项表达式;

D=A'B'(Bin)+A'B(Bin)'+AB'(Bin)'+AB(Bin)
Bout=A'B'(Bin)+A'B(Bin)'+A'B(Bin)+AB(Bin)
D通过卡诺图无法进一步化简

Bout可以通过卡诺图进一步化简

Bout=A'B+A'(Bin)+B(Bin)
<3>选定所使用器件的类型;
与非门7400和异或门7486

<4>根据器件的逻辑功能,化简或变换最小项表达式;
D=A'B'(Bin)+A'B(Bin)'+AB'(Bin)'+AB(Bin)=A ⊕ B ⊕ Bin
异或运算有结合律
Bout=A'B+A'(Bin)+B(Bin)=[A'B+A'(Bin)+B(Bin)]''=((A'B)'(A'Bin)'(BBin)')'
<5>根据化简变换后的逻辑表达式画出逻辑电路连接图。

3、用7483构成一个四位二进制全加器,实现7+6+0=? 8+9+1=?它所能进行运算的最大数是多少?
4是最高位,1是最低位
输入:A4A3A2A1是第一个(四位二进制)数,B4B3B2B1是第二个数,C0 是最低位的进位输入。
输出:S4S3S2S1是和,C4是最高位的进位输出。
(1)7+6+0=?
7的二进制表示为0111
6的二进制表示为0110
0的二进制表示为0000
0111 + 0110 + 0000 = 1101(二进制)=13(十进制)

(2)8+9+1=?
8的二进制表示为1000
9的二进制表示为1001
1的二进制表示为0001
1000 + 1001 + 0001 = 10010(二进制)= 18(十进制)
(先计算8+1)

(3)它所能进行运算的最大数是多少?
1111(A4A3A2A1)+1111(B4B3B2B1)+1(C0 )
=1(C4)1111(S4S3S2S1)(二进制)
=31(十进制)
4、用双四选一数据选择器74153来实现三人表决电路(不用门电路)。
仿照第二次实验

数据选择器
此处Y=A'BC+AB'C+ABC'+ABC=B'AC+BA'C+BAC+BAC'
但要求不用门电路,D0D1D2D3只能连接确定的电平或A、B、C
化简Y=B'AC+BA'C+BA1
设置D0=0,D1=C,D2=C,D3=1

5、设计一个密码锁。密码锁的密码可以由设计者自行设定,密码锁有4位二进制A3A2A1A0的密码输入端和一个开锁钥匙信号B的输入端,当B=1(有钥匙插入)且输入密码正确时,允许开锁信号输出Y1=1(开锁),报警信号输出Y2=0;当B=1但是密码不正确时,Y1=0,Y2=1;当B=0时,无论密码对否,Y1=Y2=0。
<1>根据逻辑功能描述进行逻辑抽象,确定输入和输出变量
输入:输入密码:A3A2A1A0,钥匙槽B,设定密码K3K2K1K0.
输出:是否开锁Y1,是否报警Y2
记匹配结果(A3K3)(A2K2)(A1K1)(A0K0)为Q(两两对应与,再四个一起与)
真值表

Y1=QB(一个与)
Y2=Q'B(一个非一个与)

有问题处欢迎指出

