当进行数据分析的时候，会由于各种原因，包括采样时间有限、非整数周期采样等，导致出现频谱泄露的现象，这个时候就要通过窗函数来进行弥补。

我们知道，信号可以按照傅里叶级数分解为余弦信号和正弦信号，因此，当进行数据采样的时候，相当于在时域中将余弦信号与矩形窗函数相乘，即：

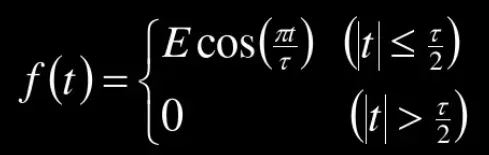
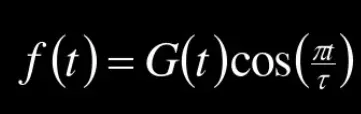
由于信号在时域相乘等于在频域卷积，因此

这可以由冲击函数的卷积性质得出：

运算过程如下：

矩形窗函数的时域和频域特性如下：

由于余弦函数的频谱是冲击序列，因此，窗函数的选取目标应该是主瓣尽可能集中，旁瓣尽可能小，以维护这种频谱性质。除了矩形窗之外，常用的窗函数还有：海宁窗等。

矩形窗主瓣窄，旁瓣大，频率识别精度最高，幅值识别精度最低，如果仅要求精确读出主瓣频率，而不考虑幅值精度，则可选用矩形窗。