数学老师做题时脑子里在想什么?

看这个视频,我自己都想出视频了,但是出视频太麻烦了,所以写个爽文好了。
写完文章之后再来写上这一句:这篇笔记值一万块钱。
两位老师的发言都非常有代表性,视频里有些关键词也是我经常讲题时提到的。我们先分析一下视频里的做题过程:

为什么数学老师这里会想到方程组呢?
我们平常在讲解析几何的时候,经常会提到“翻译”这个词,所谓的翻译就是把题目里的自然语言(即带有阿拉伯数字的汉语)翻译成数学语言(即边角关系、函数关系、方程、不等式等),我们常说一个条件能得出一个关系(方程不等式等),这些关系(方程不等式等)联立起来,就可以得到问题的答案。
那么视频里女老师看到了两个已经给你翻译好的条件,只需要让你化简整理的条件,那自然就要去化简整理啊。
有没有更深层次的原因?
14:35 时男老师说了,很多学生是不敢试错的,很多学生不敢选一个方向进行计算。女老师说如果一个学生敢想敢写敢做的话,那可能就能写出来正确答案,此时男老师回复说这就是天赋。
嗯,我们就着这条线,分析一下这个天赋是怎么来的。
为什么有那么一批人就是勇,明明不知道自己现在做的是什么,结果会是什么,就是敢想敢写敢做呢,他不怕花费精力之后一无所获吗,他不怕在考场上浪费时间吗?
这里面有性格的原因,而性格的形成一方面靠先天的基因遗传变异,一方面靠后天的环境培养。
(
-等等,我们是数学物理老师啊,怎么提到性格了,现在不是在讲题目吗?
-呃,如果搞教育只是讲题目,那为什么要设置教育心理学这门课程呢?
)
先天因素我们不提了,这里常见的例子就是“虎父无犬子”“老鼠的儿子会打洞”等谚语,人家天生就是这么勇,人家就是骨子里一点儿水分没有,就是干,你不服不行。
我们来分析后天因素。
单纯分析题目的话,后天因素有下面加粗文字的这些:
- 经验型:我遇到过太多这种情况了,虽然我看不出这个东西算下去会有什么结果,但是根据以往做题(比如视频里提到的做例题)的经验,这个东西算下去,肯定是有用的,说不定算到哪一步,我就有解题思路了,或者说不定算着算着,答案就做出来了;
- 无奈型:闲着也是闲着,不算下去,难道还干看着?
- 一眼看透型:妈个鸡,这条件要是解不出东西来,出题老师喝高了吗,把这个废物条件放这里作甚?干就完了。
- ……
我们做老师的,希望学生都是1和3,例2这种学生很可能做着做着做烦了,就放弃了,就去睡觉了。
想想经验型学生的家庭教育环境是怎样的,是不是父母会教孩子做事的时候,要注意有条理之类的?比如:把杯子(碗)放到桌子里面一点,这样就不容易打翻在地了呀~
五岁的孩子发现事实的确如此之后,简单模糊地认识到了因果律,可以举一反三,意识到下一次把易碎的物品放到更不容易碰到的地方,那么就不会打碎东西了。
如果孩子父母看到孩子把碗打碎了,直接批评+体罚的话,那么这个孩子得到的是负反馈的教育,他在恐惧和疼痛中记住的东西,显然不如前者得到的东西受用。
而这仅仅是一个小小的例子,这种事情累积多了之后,你会发现,在上小学一年级之前,每个孩子的差异都是非常大的,因为从父母那里得到的东西是不一样的。甚至由于父母沟通方式的不同,每个孩子掌握的汉语词汇量都是不一样的,词汇量更丰富的孩子,显然在学校的学习社交中,可以更便利一些。
那我们设置小学课程与考察时,尽量让小学一二年级的学生都得95分以上。
我们是故意这么设计的,我们不希望孩子的家庭教育的差异在这么早就凸显出来,让后者这批孩子绝望,进而不能好好的在学校接受更为科学的学校教育。
但是这种差异早晚会体现出来,在小学的时候,大家的各种表现可能不会那么明显,但是到了青春期,从著名的“中二现象”(中二,即初中二年级)里,你可以看到家庭环境的不同,孩子的高浓度的激素刺激下表现出的行为是大不一样的。
那么到了高中呢?
可能就是面对这么一道题目,每个人习惯性得做出自己的反应。有的人会非常有自信的算下去,有的同学会觉得:我看不透,我做了也是错,(潜意识里犯错就会有惩罚,毕竟小时候犯错就被骂被打的经历太多了),还不如不浪费这个时间精力去错,事后接受惩罚(在高中很少有体罚了,这里的惩罚一般来说就是低分羞辱)就行了,反正我也已经习惯了。
同学们,如果你看到这里,能意识到你是因为过去的受过去的教育经验,受外在的影响,在做事的时候畏手畏脚,不够自信,不敢去莽一把、拼一把的话,我希望你看到这篇文章后,能主动去认真思考一下这种感觉,改变自己,从现在做起。
这是我从教育心理学的角度去分析这个问题,但是还有一类同学不是这样的,他是:
我知道这个条件有用啊,我特喵就是不会算,算不出来啊!!!
好的,那这个问题就是纯数学问题了。
emmm,你算不出来你怨谁啊?
平常计算的练习,这种题做了多少了?
我随便翻开一本一轮复习的辅导书,都会告诉你下面类似的结论:

上面图片里的内容,就是女老师在 2:51 处说的解题思路:

而这个截图前几秒的时候,一条弹幕说从这里开始看不懂了。
接下来,我要化身邪恶,开始咄咄逼人了。
我想问一下,计算题真的需要懂吗?
你是在计算啊geigei,你既然一轮复习的时候就知道了这些条件要用a1和d表示出来,那么剩下的就是计算啊。
什么?你不懂原来这东西是要用a1和d来表示的,那你知道什么是等差数列吗?
如果你连这些东西都不知道,那么这题你就活该不会,你就活该考低分!
你自己想一下,平时但凡有认真学,认真练,这些东西你都想不到?
如果你平常学习就那么个态度,考试的时候还能让你把题目做出来,原因要么是出题老师出的题目没有任何区分度,要么就是老天爷瞎了眼。
不要装出一副一直都在教室里跟着大家一起努力学习的样子,演给谁看呢?自己到底有没有用功,自己心里没数?你是在思考,还是在放空,自己不清楚?
少在数学老师面前表演努力,你对一道题目一个知识点的理解程度到了什么地步,你花了多少时间和精力,我能看不出来?
有些题目,注意,是有些题目,题目条件给的是真的晦涩,是真的让大部分没经验的学生想不到题目条件之间有什么联系,比如前几天我讲的这道难题:
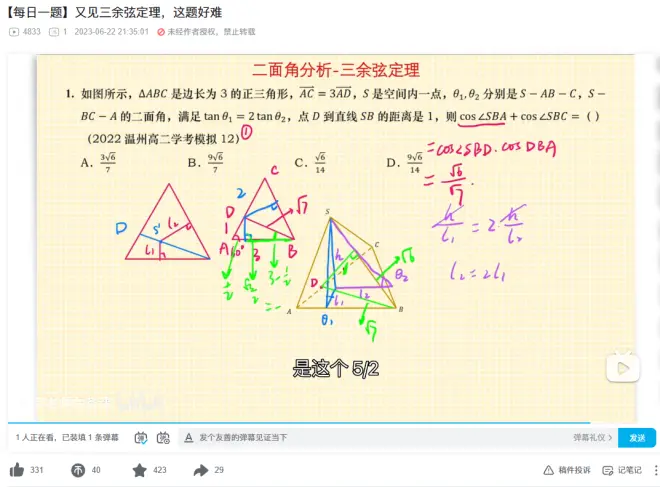
这道题目里的条件就像是一块块隐藏了棱角的拼图,你必须分析每一个条件把隐藏的棱角算出来,才能对比两块拼图的缺口,把最终的图案拼接出来。
然而视频里这个数列题,用到的思想是最基本的思想,计算也是初中生的计算。
我希望不会做的同学,不要那么理直气壮地说自己不会,仿佛是老师讲题不体谅学困生似的,仿佛就是老师讲的不行似的,仿佛你不会是别人的错似的。
这种题目不会,就是学新课或者一轮复习的时候偷懒了,这种题目不会做,绝对不可能是老师的因素!
你但凡多看看一数赵礼显佟大大的免费课,你都应该会。
如果这个第一问,都要从最基本的性质,开始给你讲起,那么这节课还讲不讲别的题目了?一套卷子讲下来得花多长时间呢?
如果你第二问不会做,原因可能是平常“以练代学”的模式:虽然计算了很多题目,但是没有老师带领着思考到底计算从何而来,而又要到何处去。
但是第一问的话,抱歉,这样的锅,数学老师不背。
接下来,讨论解题思路。
综合法与分析法?
综合法与分析法是我们在学习推理与证明时,接触到的两种思考方式。
综合法简单来说就是综合考虑题目所给的条件,把这些条件翻译、整理、化简、联立、解析出最终的答案。
分析法简单来说就是从问题出发,分析解决问题需要什么样的充分条件,一步步的往前推导,直到推导出题目给出的条件。
简单举个例子,综合法就是:如果我想年入百万,那么我要看我现在有什么基础,怎么样利用这些基础,一步步达到我的目标。
分析法就是:如果我想年入百万,我得看看年入百万需要什么样的条件,进而一步步分析出我现在能做什么。
视频里,男老师主张的是分析法,是从问题入手,分析要解决这个问题,到底是要解出什么,我应该是先去找什么做什么。
女老师用的是综合法:把给的条件整理出来,算着算着,答案就出来了。
我根据视频内容分析,男老师应该是物理老师,好奇怪啊,我记忆里解高中物理大题的时候,我用的都是综合法啊,一个关键条件对应一个方程,多个条件联立成方程组,方程组解出来,就是答案。那时候物理分析大题有一个算一个,都是解方程,就是送分题,比数学简单多了。
物理我们先不提,先说一下这两个方法。
这两个方法本来是用在证明不等式的题目中的,而用在这种解答题里,这两个方法与其说是方法,不如说是思想。
为什么这么说呢,做大多数证明题的时候,我们是知道要证明的结论是正确的,你不管正着推,还是逆着推,只要步骤没错,是一定能证出来的。
而解答题不一样啊,如果题目的答案是无解的话,那么分析法就失效了。
那为什么我们依然可以在解答题中使用分析法的思想呢?
因为我们高中数学题目都是设计好的有答案的。
这句话我在做每日一题时强调过几次,很多所谓的妙的方法,秒杀的方法,之所以能用,是因为题目设计好的,才能让你用上,假如出题老师发发狠,这些套路都得失效,这时候你就是得乖乖的使用综合法的思想,一步步从条件出发,看看自己能走多远,能不能走到答案那一步。
不管从什么角度来说,我都是支持女老师的做法的:平常练习,优先考虑综合法。
就好像我们平常讲究选择题小题大做,而不是只讲更为简单的排除法。
分析法是根据解出答案的思想,不是学习的思想。
当然,这只是平常练习的时候,真正高考的时候,以分数为先,你爱用哪个用哪个,能得分就行。你滚笔扔橡皮,都能蒙对选择题的话,我也愿称之为天降正义。
不管是学习中,还是生活中,我们很多问题是没有答案的,我们所能做到的,只能是根据我们手头上有什么,就去做什么。
分析法是仰望天空,综合法是脚踏实地。
如果是18岁的我,我也会不顾一切仰望天空。可早已不是18岁了,我现在主张先脚踏实地不踩空,再去仰望天空。

