平面几何题目分享（15）一个问题，八个外心

如图，△ABC外心O，P为其内部一点，△BOC外心为D，类似定义E，F；三角形OEF外心为K，类似定义L，M，过KLM三点的圆与圆O交于R，S两点，圆心为O₁，求证：∠O₁SR=3∠OSR。

这个问题较为复杂，篇幅原因，思路就不写那么详细了，我们将这个问题分为几个引理来证明。

引理一：△ABC外心O，P为其内部一点，△BOC外心为D，类似定义E，F，则对DEF，OP互为等角共轭。

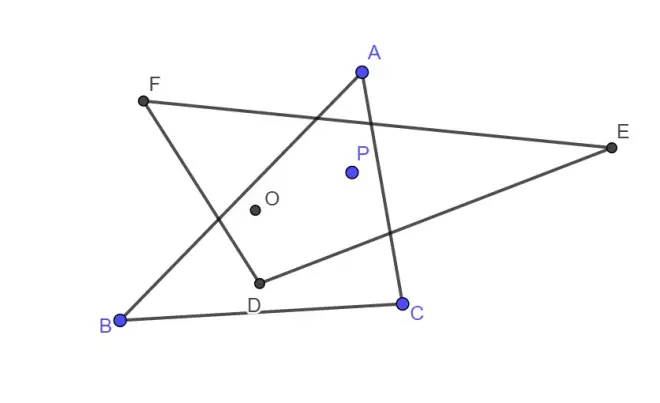
证明：由于D，E均为外心，所以直线DE是PC的中垂线，所以∠PDC=2∠PDE，又因为D是△PBC外心，所以∠PBC=1/2∠PDC=∠PDE，又因为O为外心，所以OD垂直平分BC，所以∠PBC=∠ODF=∠PDE。同理，∠OFD=∠PFE，所以OP互为等角共轭。

引理二：△ABC外心O，P为其内部一点，△BOC外心为D，类似定义E，F；三角形OEF外心为K，类似定义L，M，则△ABC位似于△KLM。

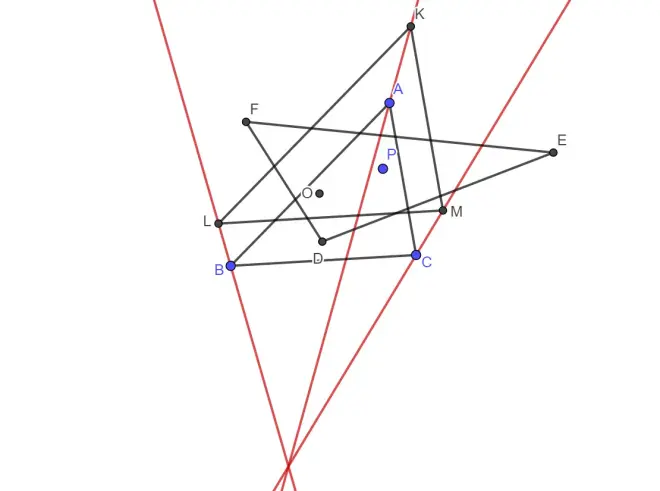
证明：只需证对应边互相平行。因为LM分别为△FOD，△ODE外心，所以LM是OD中垂线，又因为OD垂直于BC，所以LM∥BC，同理可证其余两组对应边平行，由平行易得位似。

引理三：P，Q是△ABC的一组等角共轭，△PBC外心为D，类似定义EF，求证：圆（DEF）与圆（ABC）的根轴垂直平分PQ

证明：做△QBC外心K，类似做出L，M，倒角易得∠OCD=∠OKC，所以OC²=OD*OK。即DK互为反像（反演中心为O，反演半径为OC）同理，M，F；E，L均互为反像，所以圆（DEF）的反像为圆（KLM）。即圆O,圆（DEF）,圆（KLM）共轴。

注意到OD*OK=OL*OE=OF*OM，于是有KDLE，ELFM，MFDK三组四点共圆。所以KL，DE，GH三线共点J（根心）；ML,EF,GH共点I。由外心，DE是PC中垂线，KL是CQ中垂线，所以J是△QPC外心，同理I为三角形APQ外心。所以IJ是PQ中垂线，即GH垂直平分PQ。

回到原题，由引理一，OP互为三角形DEF的等角共轭，由引理二，△KLM位似于△ABC。

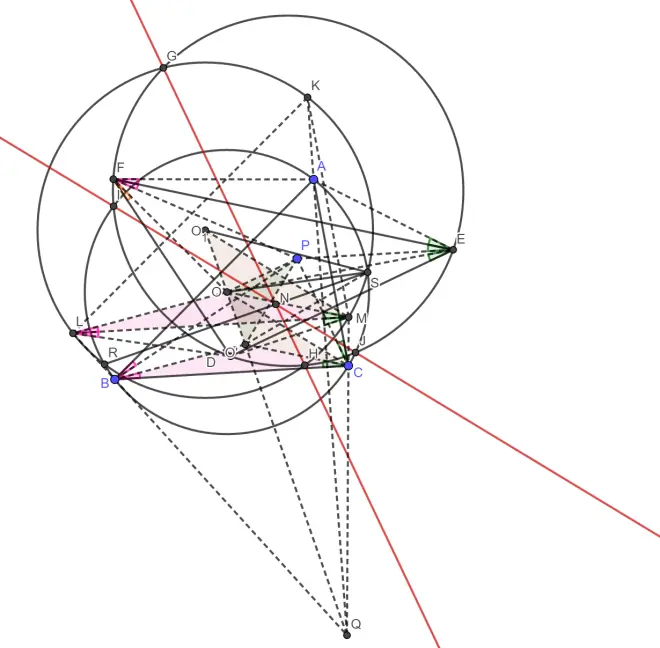
做P关于△ABC的等角共轭O’由引理三，圆（DEF）与圆O的根轴IJ垂直平分PO’，同理，HG垂直平分OP所以三圆根心N是△OO’P的外心。由外心及等角共轭，倒角易得所有绿色角和粉色角相等，所以△BO’C位似于△LOM，且位似中心与△ABC和△KLM的位似中心相同（点Q）。再由OC，O₁M均为半径，易得△OCO’位似于O₁MO，位似中心为Q。所以O₁OO’共线即OO’⊥RS。再由△OO’P的外心N在RS上，所以OO’关于RS对称。由角平分线定理，易得∠O₁MO=∠OMO’，所以∠OSR=1/2∠OMO’，即∠O₁SR=3∠OSR。