前言

        在前面的文章中我已经推导了Buck、Boost和Buck-Boost三种拓扑的各元件应力，但这是在恒功输出的控制逻辑下推导的，即开关电源会以保持输出电压（或者电流）恒定为第一目标。因此根据P = V*I可知，当开关电源的输入电压Vin降低时，开关电源会尝试增大输入电流Iin以保证输出功率Pout恒定，若Vin→0V时，则会出现Iin→∞A的极端情况（Buck拓扑除外）。

        然而在主动式功率因数校正电路中，电路需要模拟电阻的行为，其控制逻辑更改为恒阻输入。因此根据R = U/I可知，当电源的输入电压Vin降低时，电源的输入电流Iin反而需要减小，特别是Vin→0V时，Iin→0A。由于行为发生了改变，因此有必要重新对各元件应力进行重新推导。

        鉴于大多数主动式功率因数校正使用的是Boost拓扑（因为Boost输入电流连续），为节省工作量吾只对Boost拓扑各元件应力公式（主要是电流应力）进行推导。本文仅提供结论，推导过程省略。

目录

1、占空比

2、电感各应力

    2.1 传输功率、模拟电阻与电感电流直流分量

    2.2 伏秒积与电感电流交流分量

    2.3 电感电流纹波系数

    2.4 电感电流峰值与有效值

    2.5 电感电流波形

3、开关管各应力

    3.1 开关管电流峰值、平均值与有效值

    3.2 开关管电流波形

4、二极管各应力

    4.1 二极管电流峰值、平均值与有效值

    4.2 二极管电流波形

5、输入电容各应力

    5.1 输入电容电流有效值

    5.2 输入电容电流波形

    5.3 输入电压纹波波形

6、输出电容各应力

    6.1 输出电容电流有效值

    6.2 输出电容电流波形

    6.3 输出电压纹波波形

正文

1、占空比

        在主动式功率因数校正（PFC）电路中有三种工作模式：连续导通模式（CCM）、临界导通模式（BCM）和断续导通模式（DCM）。其中BCM和DCM多应用于低功率的PFC，元件一般不会承受很大的应力，如何降低成本才是主要的；而大功率的PFC终究需要使用CCM。因此本文的公式是基于电路工作在CCM下推导的。

        一般而言PFC电路的输入电压Vin是变动值，如经过整流的220V,50Hz电压。以220V,50Hz电压输入为例，其电压斜率（dv/dt）的最大值约为97.7kV/s，而PFC电路的开关频率fsw至少20kHz以上。在一次开关周期内，输出电压Vin的变化量△V至多为4.89V（一阶微分近似），约占平均输入电压的2.5%，仅为纹波电压的水平。因此可以近似在一次开关周期内Vin是恒定值，即准静态。

        同时在已知输出电压Vout的情况下，预估二极管压降VD和开关管压降VQ后，可近似计算开关的占空比D（Duty Cycle）。占空比的推导基于电感在CCM下的伏秒（准）平衡，与控制逻辑无关。

        PFC电路的控制逻辑一般不会改变自己的输出电压Vout，因此只需关注输入电压Vin的变化对D的影响（此处设定Vout = 400V）。

        可以发现D与Vin呈现负线性关系，其规律为：输入电压最小、输出电压最大时占空比最大；输入电压最大、输出电压最小时占空比最小，即Dmax = D(Vin_min,Vout_max)，Dmin = D(Vin_max,Vout_min)。

        若以时间t作为自变量，Vin分别为经过整流后的220V,50Hz和110V,60Hz正弦电压，绘制的占空比的波形如下两张图所示：

        可以看到占空比波形为输入电压波形的翻转。因为输入电压在一次正弦周期内会两次触零，所以占空比也会在一次正弦周期内两次触1。

2、电感各应力

    2.1 传输功率、模拟电阻与电感电流直流分量

        这里需要对PFC的传输功率进行详细说明：虽然PFC的控制逻辑是以恒阻输入为第一控制目标，但最终仍要实现功率平衡。若PFC的传输功率与后方电路所消耗的功率不匹配，必然导致平均输出电压Vout逐渐偏离原设定值，从而违背输出电压恒定的设定。虽然根据P = V²/R可知，在变动的输入电压下恒阻输入会导致变动的传输功率，但若输入电压按照一定的周期重复，则可以计算周期内的平均传输功率Pavg。

        输入电压周期内的平均传输功率Pavg即为输入电压的有效值Vin_rms在模拟电阻Re上产生的功耗。因为Pavg = Pout（此处忽略传输损耗），所以PFC电路的模拟电阻阻值Re为：

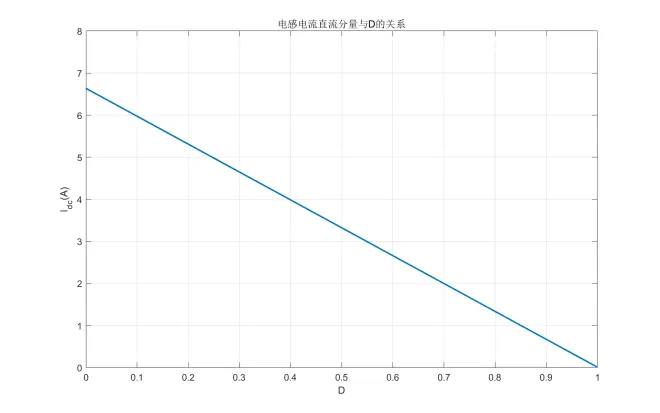
        因为在Boost拓扑中电感直接与输入端串联，所以电感电流的直流分量Idc等于输入电流Iin，再根据欧姆定律可知Idc的行为将完全复制输入电压Vin的行为，仅幅值上相差一定的系数，该系数即为模拟电阻Re。为方便后续计算，使用一定的数学手段消去Vin，得到仅有占空比D的计算式。

        通过计算式可以知道，电感电流的直流分量Idc将在输入电压最大、输出功率最大、输入电压有效值最小时达到最大值，即Idc_max = Idc(Vin_max,Pout_max,Vin_rms_min)。其中前者对应于最小的D，后两者对应于最小的Re。

    2.2 伏秒积与电感电流交流分量

        伏秒积V·t定义为电感所承受电压与所承受时间的乘积；电感电流交流分量Iac为伏秒积除以电感值L的一半。两者均与占空比有关，与模拟电阻无关。

        可以得知，伏秒积和电感电流交流分量的最大值出现在占空比D = 0.5时。因此PFC电路在低输入电压时（110V,60Hz），因为输入电压的峰值不足以使得D ≤ 0.5，所以V·t和Iac的最大值出现在输入电压的峰值时刻；而在高输入电压时（220V,50Hz），因为输入电压的峰值足够使得D ≤ 0.5，所以V·t和Iac将会呈现先变大，后变小，再变大，再变小的“M”形规律（详见2.5章节）。 

    2.3 电感电流纹波系数

        电感电流纹波系数r（ripple）定义为电感电流纹波峰峰值Ipp（两倍的Iac）与电感电流的直流分量Idc的比值。将Ipp和Idc分别代入定义式可得：

        通过观察图像可知，电感电流纹波系数与占空比基本呈正比关系，仅在占空比非常接近1的时候突然急速下降至0。这意味着随着输入电压Vin的增加，r值是逐渐减小的（忽略D = 1的邻域）。

        时刻需要记住：r > 2将意味着PFC电路进入DCM，电路若需要维持在CCM必须保证r的最大值不能超过2。通过计算式可知r的最大值将在模拟电阻Re达到最大时出现，一般为Vin_rms_max或者Pout空载的工况。同时在特定的D值达到最大值，通过以下计算式可算得特定的D值以及r的最大值。

        由于VQ与Vout相比非常小，因此α非常接近0，从而导致Dr_max→1，rmax→Re/(Lf)。

    2.4 电感电流峰值与有效值

        电感电流峰值Ipk定义为电感电流直流分量Idc和交流分量Iac的加和；电感电流有效值Irms定义为电感电流波形的均方根。通过数学手段消去Vin得：

        可以看到电感电流峰值Ipk和电感电流有效值Irms的最大值出现在D = 0的时候，其变化规律与恒功输出完全相反，并且Irms的与D的关系近似负线性，说明直流分量贡献了绝大部分的有效值。在准静态工况中，Ipk和Irms的最大值出现在模拟电阻Re最小的时候（即Pout_max和Vin_rms_min），因此需要根据最小的Re来设计电感。

    2.5 电感电流波形

        以时间t作为自变量，输入电压Vin分别为经过整流的220V,50Hz和110V,60Hz正弦电压。将Idc、Iac、Ipk和Irms绘制于同一图中，其效果如下所示：

        电感电流纹波系数r的波形如下所示：

        最终电感的实际电流波形为：

        为了让读者直观感受交流分量波形，对开关频率fsw进行了低于实际频率的夸张处理。若以真实的开关频率绘制（仅绘制半个正弦周期），其电感电流波形为：

3、开关管各应力

    3.1 开关管电流峰值、平均值与有效值

        开关管电流峰值IQ_pk等同于电感电流峰值Ipk。根据Ipk的规律，其IQ_pk的最大值将于Dmin、Re_min的工况下出现，等效于Vin_max、Pout_max和Vin_rms_min。

        开关管电流平均值IQ_avg定义为电感电流直流分量Idc乘以占空比；开关管电流有效值IQ_rms定义为开关管电流波形的均方根。通过数学手段消去Vin得：

        IQ_avg和IQ_rms的最大值均出现在Re最小的准静态工况。同时对于最大值的所在的占空比D和最大值由以下式子计算获得。

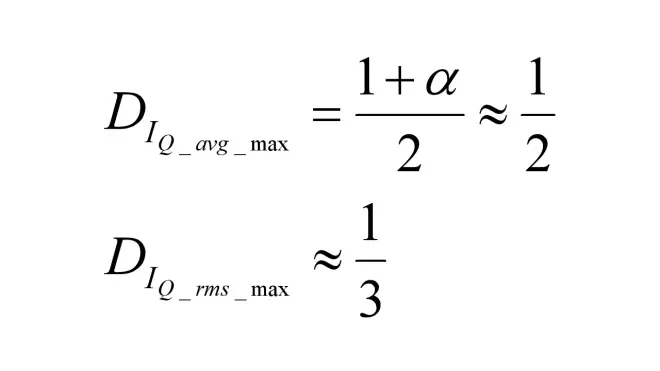
        由于IQ_avg和IQ_rms的准确值计算非常繁杂，并且VQ与Vout相比非常小，因此给出近似值。通过此可以发现两者的应力出现位置大不相同，IQ_avg的最大值出现在D ≈ 0.5的位置，而IQ_rms的最大值出现在D ≈ 0.33的位置，并且有效值比平均值大约1.54倍。在选用开关管的时候，需要根据开关管的类型而选择IQ_avg还是IQ_rms计算开关管的导通损耗。

        需要提醒：这里计算的是准静态工况下可能达到的最大值，但在实际电路中，该最大值的准静态工况不一定出现。并且就算准静态工况出现，其也是维持非常短暂的时间，最终开关管所体现的IQ_avg和IQ_rms并不会如此之大，直接根据图3.1.5计算并选用开关管是一个较为保守的设计。

    3.2 开关管电流波形

        为以时间t作为自变量，输入电压Vin分别为经过整流的220V,50Hz和110V,60Hz正弦电压。将IQ_avg、IQ_rms和IQ_pk绘制于同一图中，其效果如下所示：

        最终开关管的实际电流波形为：

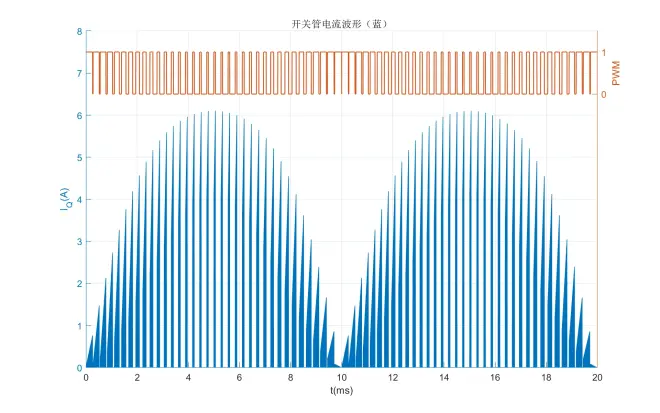
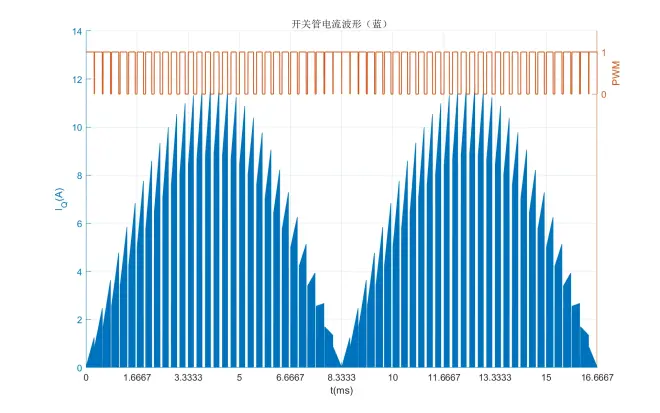
        与电感电流波形一样，为了让读者直观感受开关跳变波形，对开关频率进行了低于实际频率的夸张处理，同时波形图像改为颜色填充。

4、二极管各应力

    4.1 二极管电流峰值、平均值与有效值

        二极管电流峰值ID_pk等同于电感电流峰值Ipk。根据Ipk的规律，其ID_pk的最大值将于Dmin、Re_min的工况下出现，等效于Vin_max、Pout_max和Vin_rms_min。

        二极管电流平均值定义为电感电流直流分量Idc乘以负占空比；二极管电流有效值定义为二极管电流波形的均方根。通过数学手段消去Vin得：

        ID_avg和ID_rms的最大值均出现在Re最小的准静态工况，以及D最小的动态工况，即Re_min和Dmin。其最大值为：

        在此提醒：图4.1.4中所计算的最大值为D = 0时候的值，但在实际的PFC电路中很少达到（一般也不允许达到）D = 0的情况，因此直接按照图4.1.4计算的最大值选用二极管是一个较为保守的设计。

    4.2 二极管电流波形

        为以时间t作为自变量，输入电压Vin分别为经过整流的220V,50Hz和110V,60Hz正弦电压。将ID_avg、ID_rms和ID_pk绘制于同一图中，其效果如下所示：

        最终二极管的实际电流波形为：

        与开关管电流波形一样，为了让读者直观感受开关跳变波形，对开关频率进行了低于实际频率的夸张处理，以及波形采用填色方式绘制。

        观察图4.2.1和图4.2.2的ID_avg可以发现，其形状甚似带有直流偏置的余弦波，其实它为正矢函数，即versine(x) = 1-cos(x) = 2*sin²(0.5*x)。根据能量守恒，正弦波形的电压在恒阻负载上产生的功率为正矢波形，而又因为输出电压为常数，所以输出平均电流等于功率波形，同样为正矢函数。

5、输入电容各应力

    5.1 输入电容电流有效值

        输入电容将对电感电流的交流分量进行旁路，鉴于PFC电路的工作要求，输入电容不得将低频交流分量（50Hz）进行旁路，只能将开关频率（>20kHz）以及各类寄生振荡（>1MHz）的高频交流分量旁路（即容量不得太大）。输入电容需要能够承受电感电流中的高频交流分量有效值ICin_rms_HF。

        可以看到输入电容高频电流有效值ICin_rms_HF的最大值出现在D = 0.5的时候，其规律与Iac相似，与模拟电阻Re无关。

        需要注意，这里仅计算了高频电流的有效值，并没有计算低频电流的有效值。低频电流来自于输入电压Vin本身对Cin的充放电，其有效值与Vin的波形有关。若未得知Vin的波形则无法计算出低频电流有效值ICin_rms_LF，也就无法获知输入电容电流的总有效值。不过由于PFC电路多用于正弦输入电压的场合，对于220V,50Hz输入的正弦电压，低频电流的有效值ICin_rms_LF = 220*(2π*50*Cin) ≈ 0.152A（假设Cin = 2.2μF），低于高频分量的有效值。因此在总有效值中，高频电流的有效值将占据大多数的比例。

    5.2 输入电容电流波形

        以时间t作为自变量，输入电压Vin分别为经过整流的220V,50Hz和110V,60Hz正弦电压。将ICin_rms_HF绘制于图中，其效果如下所示：

        最终输入电容的实际电流波形为（已包含低频电流分量）：

        同前，为了让读者直观感受开关跳变波形，对开关频率进行了低于实际频率的夸张处理。

    5.3 输入电压纹波波形

        由于高频电流和低频电流同时对输入电容作用，电压纹波分量具有充放电分量和ESR分量（以及ESL分量，此处忽略），以及PFC电路输入端的EMI滤波器对不同频率分量具有不同的阻抗，其输入电压纹波是由多个因素的相互作用产生的结果，其计算相比普通恒功输出电源困难。因此此处暂不给出计算式，仅提供输入电压纹波波形。

        同上以时间t作为自变量，输入电压Vin分别为经过整流的220V,50Hz和110V,60Hz正弦电压。由于降低开关频率会导致计算出错误的纹波电压，所以此处将以真实的开关频率进行绘制。

        注：图像由输入电容电流波形进行积分后，经过4阶、截止频率为2kHz的高通数字滤波器后得到。

6、输出电容各应力

    6.1 输出电容电流有效值

        输出电容负责将二极管脉冲电流平滑，因此其需要进行大幅度的充放电。输出电容需要能够承受二极管高频脉冲电流的有效值ICout_rms_HF。

        可以看到输出电容高频电流有效值ICout_rms_HF的最大值出现在D ≈ 0.25的时候，其规律与IQ_rms相似，在模拟电阻Re达到最小值时ICout_rms_HF达到最大。

        需要注意，这里仅计算了高频电流的有效值，并没有计算低频电流的有效值。低频电流来自于二极管平均电流，其有效值与ID_avg的波形有关。若未得知ID_avg的波形则无法计算出低频电流有效值ICout_rms_LF，也就无法获知输入电容电流的总有效值。不同于输入电容，输出电容电流的总有效值中，低频电流的有效值反而占据大多数的比例。

    6.2 输出电容电流波形

        以时间t作为自变量，输入电压Vin分别为经过整流的220V,50Hz和110V,60Hz正弦电压。将ICout_rms_HF绘制于图中，其效果如下所示：

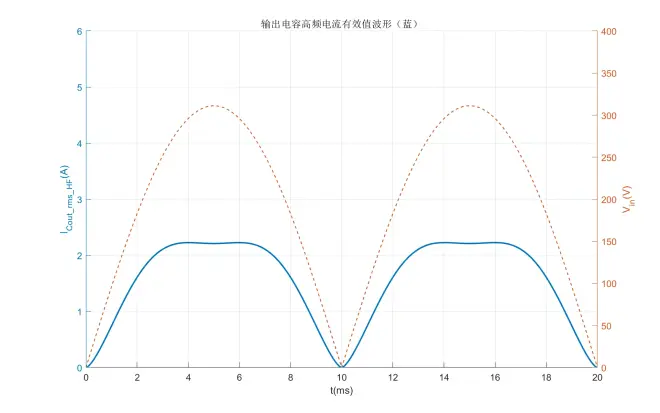
        最终输出电容的实际电流波形为（已包含低频电流分量）：

        同前，为了让读者直观感受开关跳变波形，对开关频率进行了低于实际频率的夸张处理，以及采用填色方式绘制波形。

 

    6.3 输出电压纹波波形

        由于二极管脉冲电流同时具有高频分量和低频分量，电压纹波分量具有充放电分量和ESR分量（以及ESL分量，此处忽略），以及负载端对变化的电压有不同的阻抗，其输出电压纹波是由多个因素的相互作用产生的结果，其计算相比普通恒功输出电源困难。因此此处暂不给出计算式，仅提供输入电压纹波波形。

        同样以时间t作为自变量，输入电压Vin分别为经过整流的220V,50Hz和110V,60Hz正弦电压。由于降低开关频率会导致计算出错误的纹波电压，所以此处将以真实的开关频率进行绘制。

        注：图像由假设负载为CC负载并对输出电容电流波形进行积分后得到。

后记

        本文乃Buck、Boost和Buck-Boost三种拓扑的各元件应力文章的举一反三之作。由于参考书籍并没有对此类情况进行分析与推导（指高频电流部分，低频电流详见书本的14.3章节），因此吾只能自行编写仿真程序用计算机计算并绘制波形，再与公式所绘制的图像进行比对，以校验公式的正确性。若读者发现公式或图像错误之处，欢迎在评论区予以指出纠正。

参考书籍：[美]Sanjaya Maniktala 著, 王建强等 译. 精通开关电源设计[M]. 中国工信出版集团, 人民邮电出版社；

使用MATLAB绘制图像。

 

by HD-nuke8800

编写完成于： 2023/07/12