【高等数学第15讲】拉格朗日中值定理

第十五章 中值定理（3）——拉格朗日中值定理【最重要、最核心】

一、知识点

1. 拉格朗日中值定理：
   

   04:05

   
2. 内容：
3. 条件：①[a,b]上连续；②(a,b)内可导
4. 结论：则存在ξ属于(a,b)，使得f'(ξ)=(f(b)-f(a)) / (b-a)
5. 几何直观：
   

   05:21

   
6. 注解：
7. 拉格朗日加上"f(b)=f(a)"的条件就退化成罗尔定理。
   

   12:47

   
8. 拉格朗日中值定理的几个等价形式：
   

   13:32

   
9. f(b)-f(a)=f'(ξ)(b-a), ξ属于(a,b)
10. 任意x,f(x)-f(x0)=f'(ξ)(x-x0), ξ位于x与x0内部
11. 有限增量公式：f(b)-f(a)=f'[a+θ(b-a)](x-x0), 0<θ<1.
12. 若函数在[a,b]连续，(a,b)可导，且f'(x)恒等于0，则x在区间[a,b]上，f(x)是常函数。
    

    20:42

    
13. 关于拉格朗日中值定理最常用的几个基本思路：
14. 基本思路1：
    

    28:30

    
    （差值）
15. 见到两点函数值 或 f(b)-f(a) 或 (f(b)-f(a))/(b-a)，想到用拉格朗日
16. 基本思路2：
    

    54:18

    
    （沟通相邻阶导数，0阶就是原函数）
17. 沟通f与f'（或f'与f''）
18. 基本思路3：
    

    60:41

    
    （（三点函数值，用两次拉格朗日）
19. 三点函数值（或者四点），主要是阶数相同，使用两次拉格朗日
20. 如果两项的复杂度不同，先搁置简单项，还原复杂项
    

    01:09:16

    
21. 还原之后有可能用到拉格朗日，也有可能用到柯西
22. 几个重要结论：（见图1）（记）

图1：几个重要结论

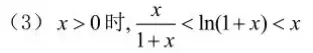
二、证明

1. 证明拉格朗日中值定理：
   

   07:44

   
2. 证明“若函数在[a,b]连续，(a,b)可导，且f'(x)恒等于0，则x在区间[a,b]上，f(x)是常函数”：
   

   21:42

   
3. 证明“arcsinx+arccosx=π/2”：
   

   25:15

   
4. 用拉格朗日注解3证明
5. 用基本思路1证明不等式：
   

   36:35

   
6. 证明几个重要结论：（使用拉格朗日中值定理证）
7. 

   40:10

   
8. 

   42:41

   
9. 

   47:15

   
10. 用基本思路2的证明题：
    

    55:45

    
11. 用基本思路3的证明题：
    

    01:02:14

    
12. 又忘了介值定理求出的ξ是在闭区间上的
13. 用基本思路3的证明题：
    

    01:12:04

    
14. 使用基本思路3(2)的证明题：
    

    01:18:36

    
15. 含ξ、η的项复杂度不同=>η复杂=>集中η

三、计算

1. 使用基本思路1求极限：
   

   30:04

   
2. 注意细节，体会一下做题步骤