蒙特卡洛光线追踪基础 - 渲染方程与概率密度函数

欢迎来到我的专栏。经过前面几次杂谈瞎掰之后,我又想回来写点偏技术的东西了。
这里,我想使用极短的篇幅来介绍一下我们现在做光线追踪的一些技巧。希望对您有用。
现在这个年代,您应该多少对光线追踪和全局光照有所耳闻。没错,当前的计算机实现全局光照最准确的方法就是光线追踪。

而我们现在所指的光线追踪实际上是路径跟踪(Path Tracing),它是建立于 1986 年 James Kajiya 老先生所提出伟大的 “渲染方程(The Rendering Equation)” 的基础上的。
并且,渲染方程从 1986 年指导了整个渲染领域至今。我们现在做的一切工作都是为了逼近或者直接求解渲染方程,以此达到照片级真实感。(不过令琪老师他们的波光体系的论文最近也发了,估计不久以后图形学光传输理论领域也要变天了)
最早比较完备的光线追踪着色算法实际上是 Turner Whitted 于 1979 年提出的经典递归光线追踪模型(Whitted-Style Raytracing)。
Turner Whitted 仍健在,并且现在正在 NVIDIA Research 任职!
经过了这十几年通用算力不断膨胀,实时光线追踪也开始逐渐成为了热门话题。然而,目前的 GPU 算力仅仅只能支撑起我们做很小一部分的光线追踪,每一次发射光线我们都不能保证完全得到想要的信息。

无论是实时游戏里的还是离线渲染器里的光线追踪,本质上它们都是一个东西。只不过是采样率上存在差别。
好了,历史课上完了。接下来的东西就有点头疼了哦。

首先,

这个图形象地概括了渲染方程地核心思想。其实它还可以用 来概括,意思是从光线到摄像机,光线在传播途中可以进行多次的 Diffuse 和 Specular 的反弹。
为了方便,这里稍微省略一下括号内的自变量(不代表它们不存在),则每条光线的能量传输都可以写成:
至于整个半球空间内,一个点接受到四面八方来的所有光线的累积就是:
不过这只是反射的出射光线。加上自发光的话,则是:
为了统一和舒服起见,以后我们都使用以下形式的渲染方程:
其中:
是最终出射光
是自发光
是双向反射分布函数(BRDF),它决定光线从某种特定表面弹射出去时会具有的一些特性(例如法线的分布),它同时是基于物理渲染(PBR)的基础
是入射光,也是上一个弹射点的最终的出射光
是入射光和法向量夹角的余弦值,并且
就是反射的其它地方来的光,半球空间用
表示
注意,渲染方程里光是规定了具体辐射能量单位的,即现实中的瓦特每平方米,这也体现出了它的物理准确性。而不像传统局部光照模型(例如 Blinn-Phong)那样只有一个笼统的,经验性的 “光强” 概念。

以上就是关于渲染方程的一些东西了。所以我们就得到了一个具体的方针——想要得到照片级画质,就求解渲染方程。
然而我们去看看渲染方程的形式,它是一个标准的积分方程。我们要如何在计算机上用数值方法去求解那么大坨定积分呢?
我们以这个定积分举例:

我们知道,这个蓝色曲边梯形的面积为:
这定积分本质上就是一个极限嘛,当然我们可以把等式右边稍微变个型,也就是
诶,不知道你发现没有,上面那张图上面的 是均匀分布的,其实这样的法则反映到我们这里就是均匀采样(Uniform Sampling)。
而 想要表达的正是通过随机均匀采样来求得蓝色曲边梯形的面积。而这样随机采样来求解积分结果的方法也叫“蒙特卡洛方法”(Monte Carlo Method),这样的积分我们也叫它“蒙特卡洛积分”。
然而你也发现了,如果要收敛到正确结果,那么我们得做无限次的采样(),这对于计算机来说显然不现实,何况我们这些做渲染的追求质量的同时的可不就是追求一个快。所以我们为了速度,一般都是大大降低了采样次数的。
在上述的 中,我们把
称作均匀采样的“概率密度函数”(Probability Destiny Function, PDF) ,所以还可以表示为
以后看到 PDF 就不要只想成文档咯 (~ ̄▽ ̄)~
所以,哈哈,我们得到了一种船新的利用概率密度函数来求积分的数值方法(虽然结果不一定收敛)
然而,均匀采样对于我们做全局光照的来说,缺点是很大的。例如,在部分信号强烈的地方和信号弱的地方做了同样的采样,这样一来效果就差了。比如下图所示的,均匀采样比余弦权重的采样噪点更多,因为根据下图余弦波瓣所示图象的特点,球顶分布的采样会比底下的更密集。
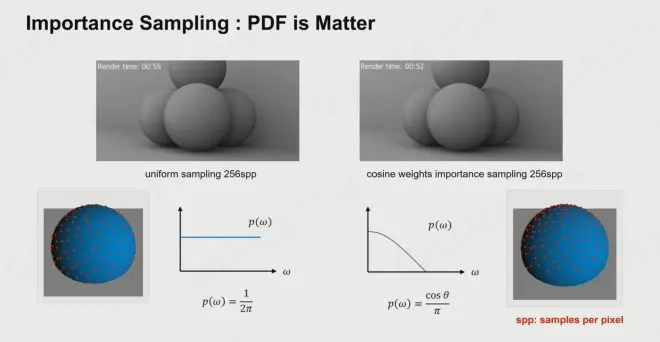
所以,使用合适的 PDF,可以更加逼近正确值。我们这里就引入一种很重要的采样方式:重要性采样(Importance Sampling)
看名字我们就知道了,这是根据重要性来进行采样,哪一部分需要集中采样,哪一部分不太需要,就是根据 PDF 决定的。这样我们可以得到比均匀采样准确得多的结果。
常见的 PDF 有 ,也有我们熟悉的老常客 GGX 分布函数,了解 PBR 的人都知道它很适合做 Specular。
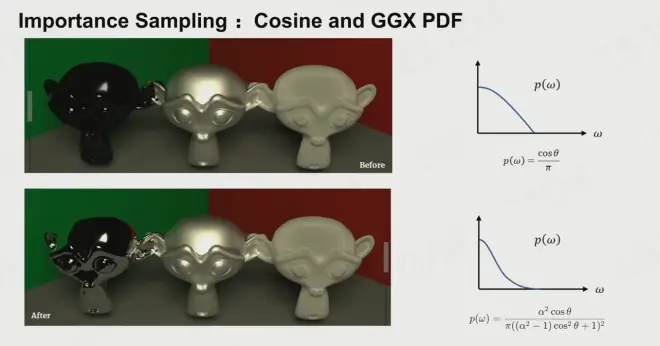
您看,像 GGX 这类概率密度分布就和余弦波瓣的就不一样,我们明显能感受到 GGX 要更急,它就可以很好地做金属表面的效果。
不过,我们不能抓住一个 PDF 不放,最重要的是根据需求而选择合适的 PDF。归根结底,做渲染也是一个做 Sampling 的过程,我们一定要选择合适的采样法则,这样才能更好地逼近于正确值,实现照片级渲染。
谢谢大家看到这里!

