GAMES101-现代计算机图形学入门-闫令琪

Games101 个人笔记（更新至Lecture6）

• 我也是刚入门的小白，记笔记主要是为了帮助自己巩固知识点，希望也能对小伙伴们造成一点微弱的帮助！
• 笔记中可能会有写错的地方，请各位大佬批评指正~~

---------------------------------------------------

Lecture2 线性代数简单总结

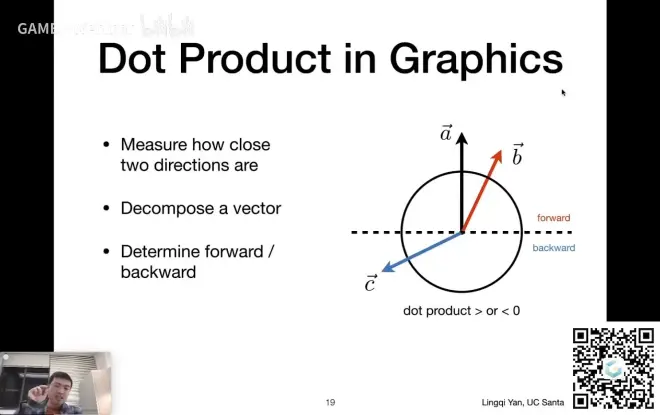
向量的点乘

可以判断向量前与后的信息

点乘>0 同方向

点乘<0 反方向

向量的叉乘

输入两个向量，输出一个同时垂直与这两个向量的新向量

如何判断新向量的方向？

右手螺旋定则

如a×b=c

四指从a的方向向b的方向握紧，大拇指指向的就是c的方向

如何判断两个向量的左右关系？

a×b得到结果是和z轴同向，是正的，说明b在a的左侧

如何判断一个点是否落在三角形内部？（做光栅化，给三角形内部的像素着色需要用到）

AB×AP > 0 说明P在AB左侧

BC×BP > 0 说明P在BC左侧

CA×CP > 0 说明P在CA左侧

说明点P落在三角形ABC内部

矩阵

矩阵的乘积

首先两个矩阵必须要可以相乘

（M x N）（N x P） = （M x P）

第一个矩阵的列==第二个矩阵的行。才能相乘

如：

第一个矩阵M行N列

第二个矩阵N行P列

得到M行P列的新矩阵

新矩阵a行b列的元素怎么得出来呢？

第一个矩阵a行和第二个矩阵b列做点积运算

如：

二行三列

5*9 +2*8 = 61

矩阵的性质

矩阵乘向量

矩阵的转置

单位矩阵、矩阵的逆

向量的点乘、叉乘（矩阵形式）

向量的点乘（矩阵形式）（见下图）

向量的叉乘（矩阵形式）

将a向量重新组织，变为A*这个矩阵，A*这个矩阵叫a向量的伴随矩阵

A*乘以b就是axb的结果

（Lecture4的罗德里格斯旋转公式会用到这个性质）

------------------------------------------------------------

Lecture3 变换简单总结

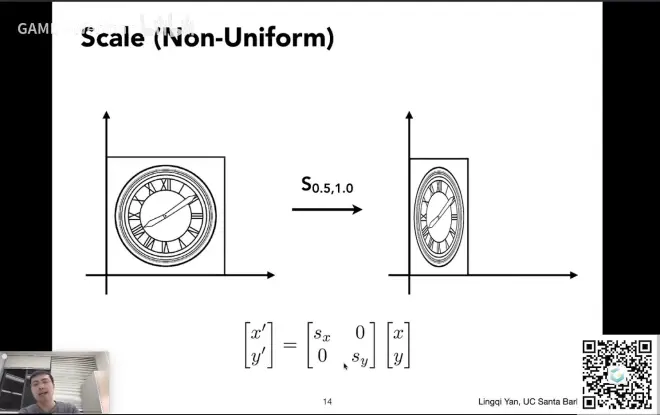
缩放变换

Sx 0

0 Sy 就叫缩放矩阵，与xy点乘得到缩放后的矩阵

镜像变换

错切变换

对于图片来说每个点的y坐标都没变

对于左上角的点来说变化应该是0+a

对于右上角的点来说变化应该是1+a

对于左边中间的点来说变化应该是0+a/2

所以每个点的变化应该是x+ay

故矩阵如图

旋转

默认绕（0，0）转，默认逆时针旋转

公式推导

如果用一个矩阵乘以输入可以得到输出的坐标，那么称这个变换叫线性变换

平移

平移可以写成

x = x + tx

y = y + ty

矩阵如图，无法写成线性变换的样子，为了解决平移这个特例，人们引入齐次坐标

齐次坐标

（齐次坐标这里老师讲的非常透彻，深入浅出，忘记了知识点的话建议直接看视频）

2D变换的齐次坐标形式

先旋转在平移写作 （T·R·向量） 从右往左写

------------------------------------------------------------

Lecture4 变换进阶篇

3D变换

3D变换相对于2D变换来说只是多增加了一个维度，可由2D变换举一反三得来

3D旋转

3D旋转在绕Y轴旋转时理解有些特殊

以xyz三个轴来说

X x Y = Z Y x Z = X X x Z = -Y

所以绕Y轴旋转的矩阵表现出来是转置的状态

罗德里格斯旋转公式

我们说在三维空间内绕某一轴旋转，默认这个轴是过原点的

罗德里格斯旋转公式就是总结了绕任意过原点的轴旋转的公式

拆分一下罗德里格斯旋转公式（下图来自百度百科）

对于绕不过原点的轴旋转，我们可以将其拆分为

1. 将旋转轴平移到原点
2. 绕轴旋转
3. 将旋转后的模型平移回去

视图/相机变换

图形学的最终目的是为了将三维中的物体渲染成二维里的图像

在现实生活中如何照一张照片？

1. 找个好地方摆pose（Model变换）
2. 把相机放个好角度（View变换）
3. 按快门（Projection变换）

View变换--如何摆放相机的角度

1. 决定相机的位置
2. 决定相机看向的方向
3. 决定相机头朝上的方向

规定相机永远在（0，0，0），沿着-Z看

变化的永远是其他物体

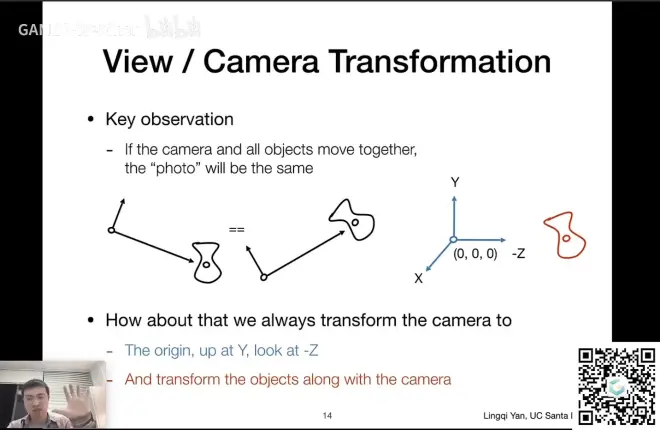
所以要先把摄像机归到原点

1. 平移摄像机至（0，0，0）
2. 将相机lookat的方向旋转到-z
3. 旋转相机头朝上的方向到Y

第一步的平移可以简单的写成下图Tview

但是要将任意向量旋转到轴上比较难写（也就是第2步和第三步）

但是将轴（如X轴（1，0，0））旋转到任意向量比较好写

所以我们先求将X轴旋转到任意向量的矩阵，之后将该矩阵求逆，即可得到任意向量旋转到轴的矩阵Rview

Rview x Tview = Mview

Mview即为视图变换，将Mview应用到相机，相机归零，同时也需要将Mview应用到其他所有物体，让物体和相机的相对位置保持不变

投影

正交投影

先将相机归零lookat -Z轴

对于二维投影来说，直接把Z轴坐标舍弃，就能得到物体在xy平面上的投影

要把得到的图像平移并且缩放到[-1,1]²中，方便之后的计算

对于正交投影来说，视口是个[l,r][b,t][f,n]的长方体,想让他变成[-1,1]³中的话只需要

• 先将立方体的中心平移到原点
• 在将立方体缩放到[-1,1]³中

首先要找到立方体的中心点，也就是

将边长r-l、t-b、n-f缩放到长度2

所以正交投影矩阵如下

（此时物体肯定会被拉伸，在之后的视口操作中会恢复拉伸）

透视投影

传统的欧式几何是在同一平面内生效的法则

对于不同平面就会造成照片中近大远小的情况

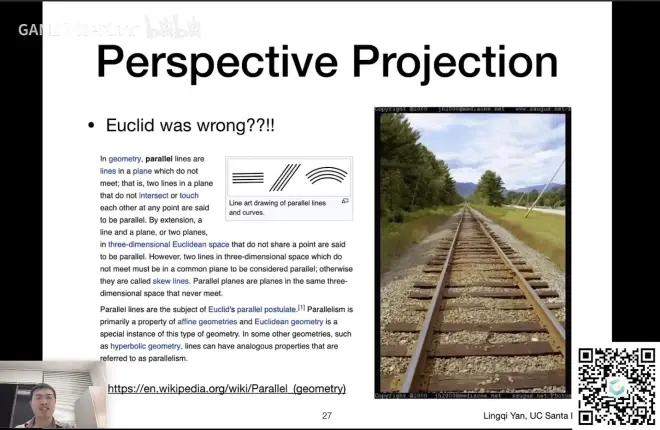
如何做透视投影呢？（本分P难点！）

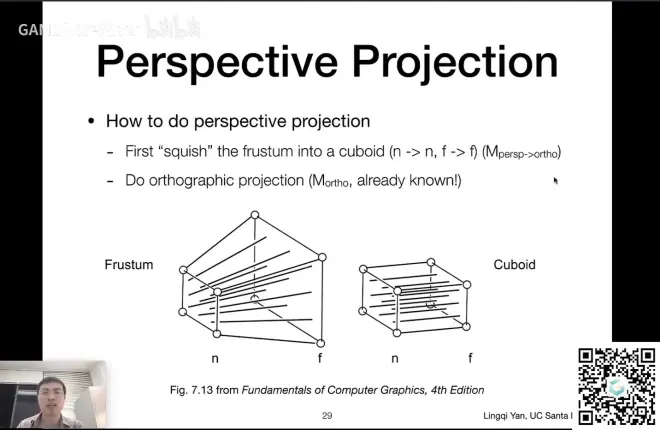
老师的方法是，先将Frustum远平面及远平面到近平面之间的所有平面挤压到近平面大小，

变成Cuboid的样子，然后做一次正交投影

那么如何做挤压呢？

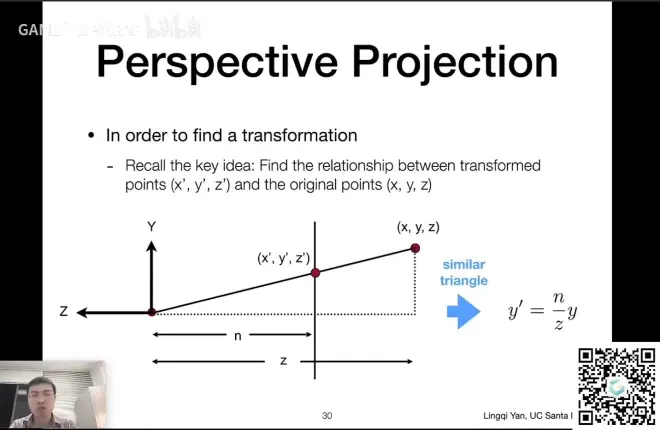
• 对于除近平面外的任意一个点，通过挤压后该点的高度y要变成和近平面一样的y’
• 从侧面看Frustum的话，如下图，可以形成两个相似三角形，即可得出y‘=(n/z)y
• 同理x'=(n/z)x

• 通过上面推导出来的两个公式可得，对于任意一点（x,y,z,1）T 可得

这里为了方便书写，用T来表示转置矩阵，下文同

将这个点同时乘z得

（齐次坐标同时乘k（k！=0），还得到相同的点）

齐次坐标的性质的复习↓（详解可见虎书150页）

• 所以我们推导出了变化后的点的一部分

就是

• 那么一个矩阵乘以任意一点（x,y,z,1）T得到上图，我们就可以推导出这个矩阵的一部分了

矩阵的一部分如下图

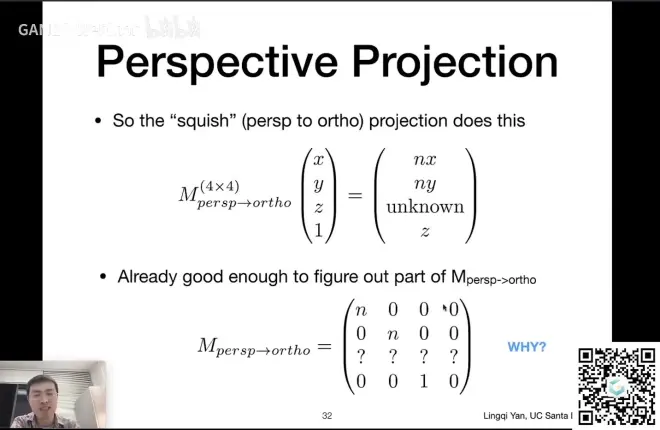
想补全这个矩阵，需要用到两条已知的性质

1. 近平面的点不会发生变化
2. 远平面的点z的值不会发生变化

• 对于近平面上的点来说，他的z值就是n

见下图

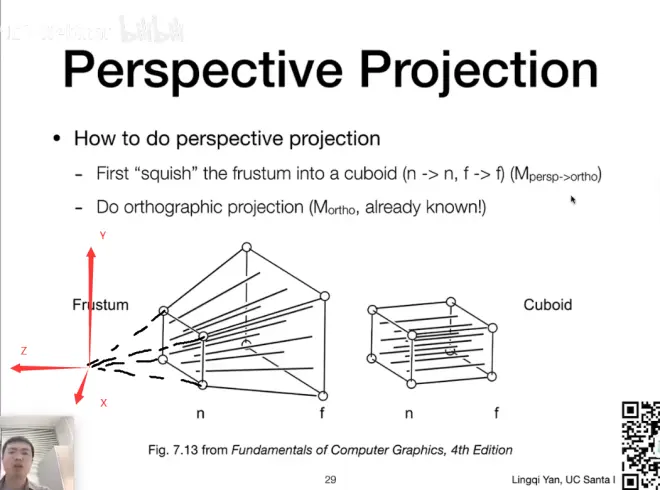
由性质1可得

对于近平面上的点（x,y,n,1）T经过矩阵变换后该点还为（x,y,n,1）T，同时乘n后得(nx,ny,n²,n）T

所以当z等于n时，也就是说近平面的点通过矩阵运算后变为(nx,ny,n²,n）T

所以矩阵第三行乘以（x,y,n,1）T= n²

可得第三行前两个数一定为0，即（0，0，A，B）

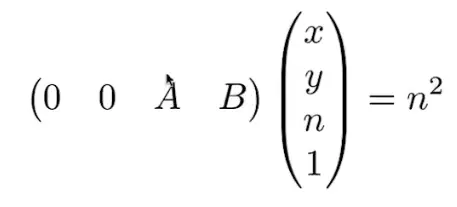
可得

1. An+B=n²

由性质2可得

选一远平面上的点x=0，y=0，即中间点（0，0，f,1）T，经矩阵变化后还是中间点（0,0,f,1）T，同时乘f后得（0，0，f²，f）T

即（0，0，A，B）(0，0，f,1）T=（0，0，f²，f）T

可得

2.Af+B=f²

联立1、2得

A=n+f

B=-nf

至此可解出Mpersp -> ortho

所以对于空间中任意一点进行透视变换可以通过如下公式解出

关于任意一点挤压后向哪里移动的问题，简单推导了一下

---------------------------------------------------------------------------------

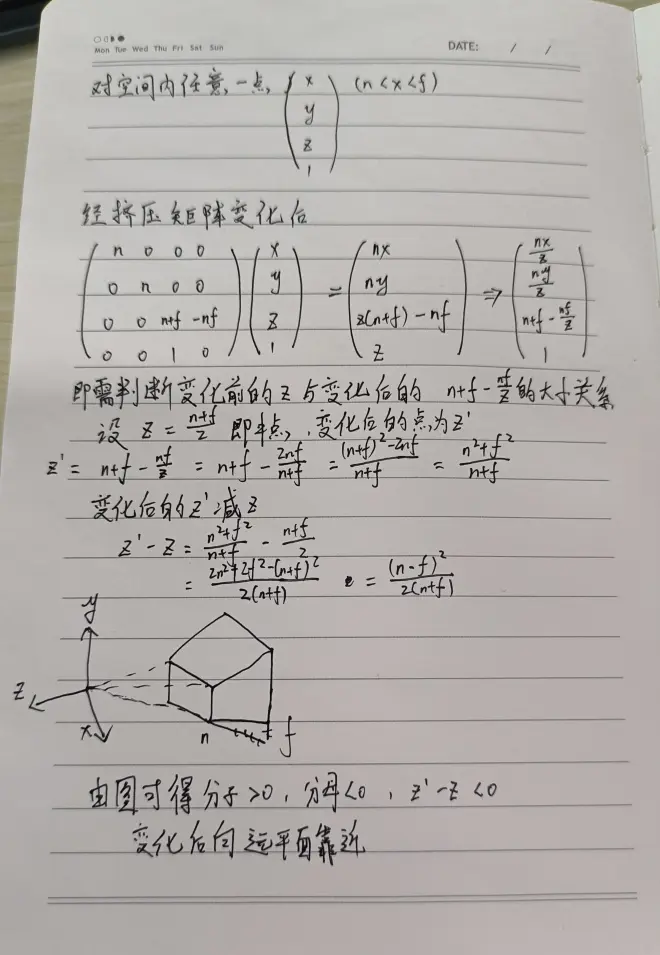
Lecture5 光栅化

在进行了上节课的操作之后，所有物体都处在了[-1，1]³的立方体中，接下来就要把他画在屏幕上，这一步就叫做光栅化

在做透视投影时候需要将一个四棱梯挤压成正方体，就需要先定义一个视锥（四棱锥）

那么如何定义视锥呢？

从摄像机看向一个地方，我们把它当作近平面，宽和高是可以定义的，所以宽高比就是可以定义的

• 宽高比 Aspect ratio
• 可视角度 FOV （垂直角度和水平角度可以互相转换）

通过以上两点即可定义一个视锥

要把图像投影到屏幕上就需要先定义屏幕，在图形学中，屏幕就认为是一个装了像素的二维数组。如数组大小1920*1080

像素是最小单位，每个像素由RBG构成

屏幕空间

屏幕坐标系如下图

像素的坐标以左下角为准，如图中蓝色像素坐标为（2，1）

像素的中心为（x+0.5,y+0.5）

继续上节课的话题

如何将[-1,1]³中的东西显示到屏幕上呢？

• 暂时忽略z
• 如果只将[-1,1]²中的东西显示到[0,width] x [0,height]，那么就很简单了

做个缩放并平移就可以，这个变换就被称为视口变换

隔行扫描

老师提到的一个有意思的知识点

以前的显示设备要成像，都是在屏幕上画很多线，画满整个屏幕就形成了一帧画面

隔行扫描就是说

在第一帧只画1、3、5等奇数线

在第二帧只画2、4、6等偶数线

利用人眼的视觉残留特性，这样人们即发现不了画面的异常，还能使机器工作量减半

如今还有某些视频压缩技术采用了这个思想

（但是隔行扫描会造成严重的画面撕裂，特别是对高速运动的画面来说）

现代的一些显示设备介绍

三角形

为什么光栅化选择了三角形？

• 三角形是最基本的多边形，没有比三角形边更少的多边形
• 其他多边形都可以拆分为三角形
• 三角形必定在一个平面内
• 容易定义三角形的里外
• 三角形的三个点定义好后，三角形内任意一点可以通过线性的插值来计算得到（重心坐标的插值方法）

如：定义好三个点的颜色，三角形内任意一点的颜色可以通过三个点的颜色来进行插值计算得到

如何将三角形转化为一个一个的像素？

简单近似采样

给定一个连续的函数f（x），当x等于1时得到的f（1）就是1的采样

所以采样就是把一个函数离散化的过程

只要有一个定义在屏幕空间的函数，那么我们就能算出来不同像素中心的值是多少

我们要采样的东西就是

给定一个三角形，在像素的中心进行采样，来判断中心是否落在三角形内

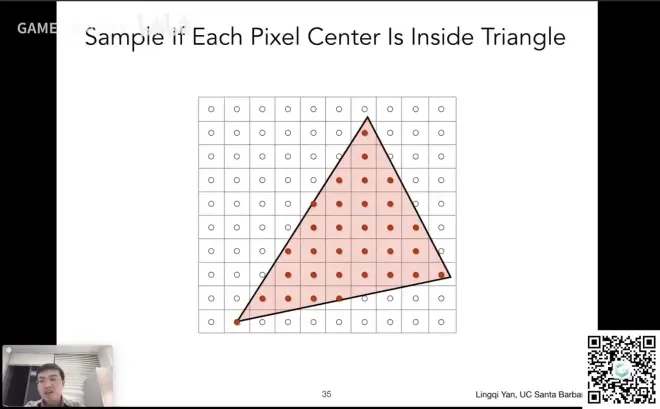
逐像素遍历，判断该像素中心是否在三角形内部，输出到屏幕显示

（至于如何判断点在三角形内部，前面的课程也讲过请看Lecture2）

但是遍历所有像素开销太大，如下图中白色那一列的像素根本没有碰到三角形，所以只要遍历蓝色区域就可以了

我们知道三角形三个顶点的坐标，有了Xmin，Ymin，Xmax，Ymax就可以得到蓝色的区域

蓝色区域就叫做包围盒（轴向包围盒/BoundingBox/AABB）

采样完成后，因为每个像素都是最小单位，像素内的颜色必须一样，所以我们会得到这样一副图

这看起来和初始的三角形差别很大，有一个个的明显锯齿（Jaggies/Aliasing）

下节课就会学习图形学中的重大技术，反走样aka抗锯齿！

---------------------------------------------------------------------------------------------------------------------------------

Lecture6 反走样&深度缓冲

采样理论

把到达光学元件上的光，产生的信息，离散成了像素，对这些像素采样，形成了照片

采样不只发生在位置上还能发生在时间上，对图像在时间上进行采样，形成了视频

采样产生的问题

• 走样
• 摩尔纹
• 车轮效应

原因就是信号的变化太快了，以至于采样的速度跟不上

反走样处理方法：采样前模糊

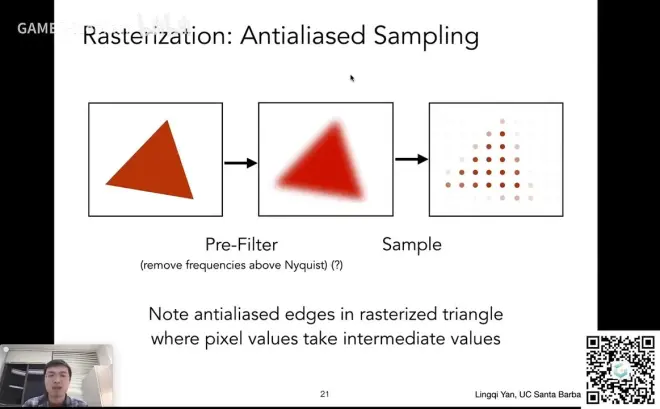
不能先采样再模糊！只能先模糊在采样

频域、时域

频域和时域是对信号或系统的两种不同的表示方式。

频域表示是通过分析信号的频率分布来表示信号的方式。在频域中，信号被分解为一系列不同频率的分量，每个分量对应着信号中的一种特定的周期性成分。

时域表示是通过直接分析信号在时间上的变化情况来表示信号的方式。在时域中，信号的变化被直接表示为在时间上的变化，而不是在频率上的变化。

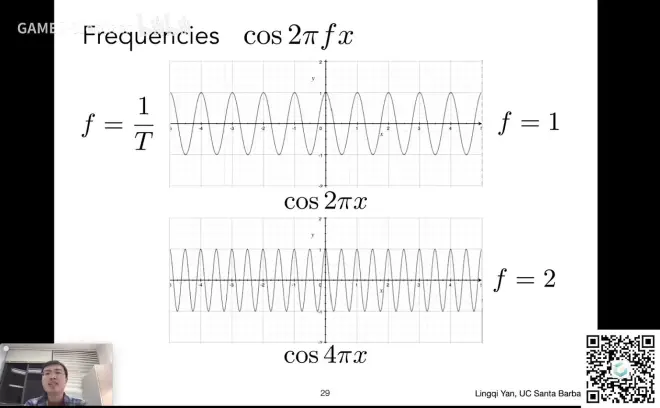
傅里叶级数展开

任何一个周期性的函数都可以变成一系列正弦/余弦的线性组合和一个常数项

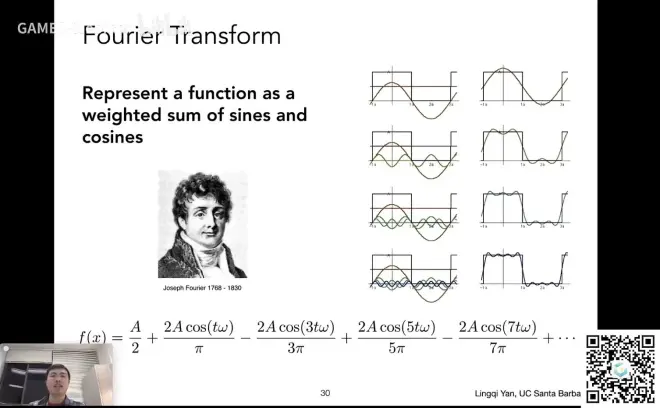
傅里叶变换

可以把一个函数f（x）通过变化变成F（w），F（w）还能通过逆变换变成f（x）

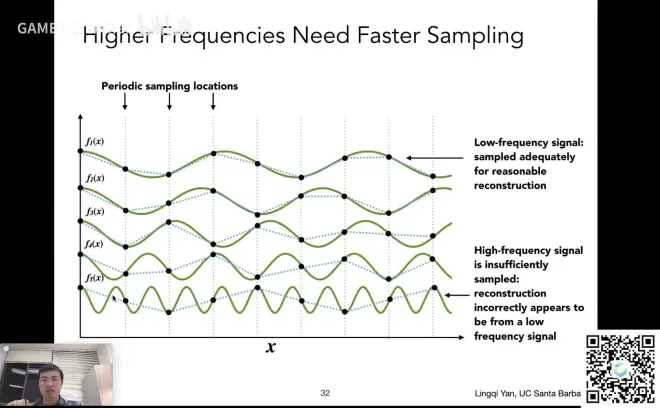
对五个不同频率的函数波形进行采样

通过f1(x)、f2(x)的采样点，我们可以大致还原出f1(x)\f2(x)的函数波形

但是从f3(x)开始，还原出的波形和原来的函数有较大出入，越往下越明显

这里就可以理解什么叫采样的频率跟不上信号变化的频率了

我们对蓝色函数进行采样，得到黑色的函数

但假如原本就有这样一个黑色的函数

我们同时对蓝色和黑色进行采样，两个截然不同的函数，得到的采样结果完全相同

这就被称为走样（Aliases）

滤波

滤波就是抹掉一些特定的频率

对应的信号如何发生变化

傅里叶变换可以把一个函数从时域变到频域

右边的图像就是左边的照片通过傅里叶变换得到的

右边图像表示的就是有多少信息

中间部分是低频信息，越往外越高频

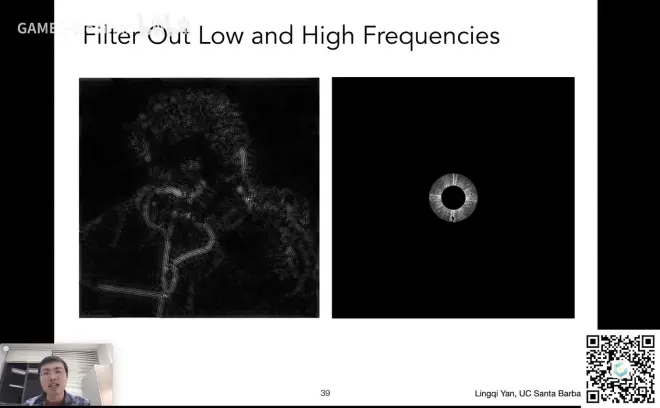
高通滤波

在频域空间内完全抹掉低频信号，将结果还原成图像，形成左图

高频的东西在图像上表示的就是图像的边界

为什么高频信息代表着边界？

当某一图像的周围突然发生发生了变化，我们就认为他是边界

比如图中人物的衣服和背景就是由黑色突然变成了灰色

相当于颜色信号突然从黑色变成了灰色，就是出现了高频的变化，即边界

低通滤波

同理高通滤波，得到模糊的图像

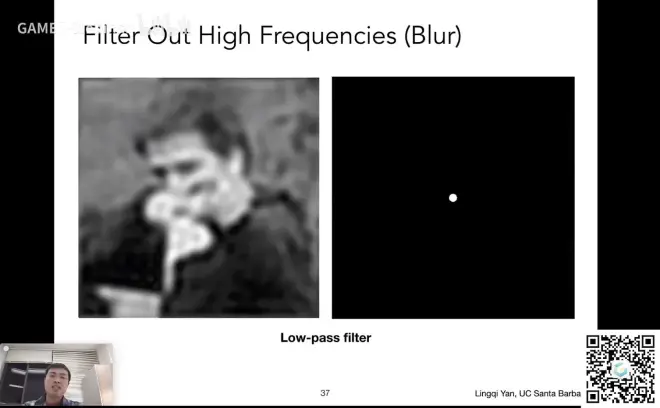
去除高频和低频，只留一部分

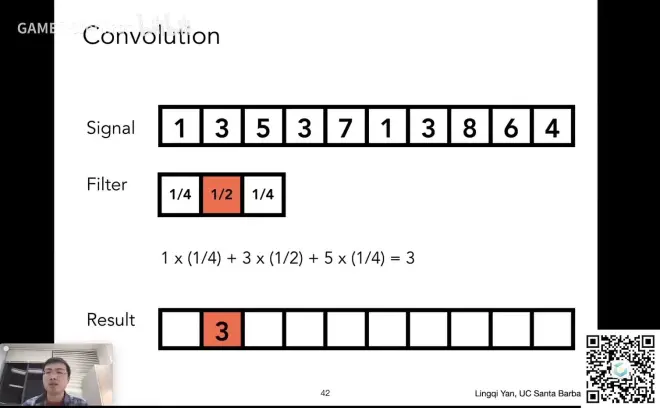
卷积

移动窗口（Filter），将窗口中三个数和覆盖信号的三个数做点乘，填到结果中

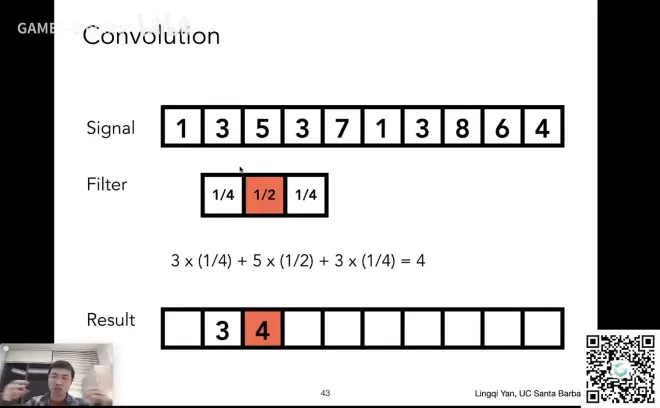
其实就是信号在任意一个地方，在他的周围做了个平均操作

卷积的一些定理

时域的卷积 == 频域的乘积

• 可以拿到一幅图直接用一个卷积滤波器进行卷积操作
• 也可以

1.先傅里叶变换这幅图，将这幅图变到频域

2.将卷积滤波器变到频域上

3.将两者相乘，乘完后得到的频域的结果，将其逆傅里叶变换，变到时域上

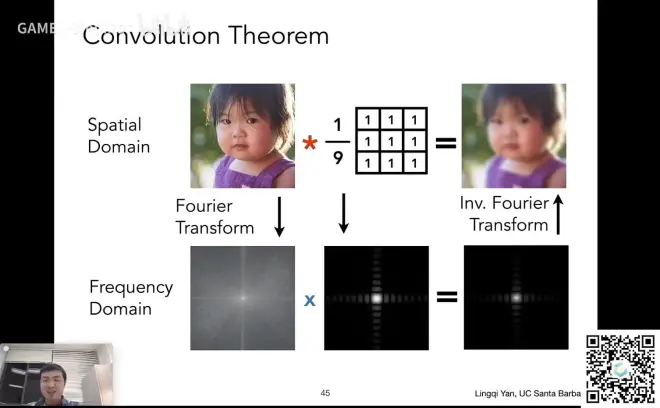
将3*3的滤波器乘1/9是为了不让图像整体的颜色发生变化

如果不乘1/9，那么每个像素就会是原来这个像素周围九个像素的和，图像就会越滤波越明亮了

时域中的图像的变化会对频域产生什么样的影响？

什么是采样，什么是走样

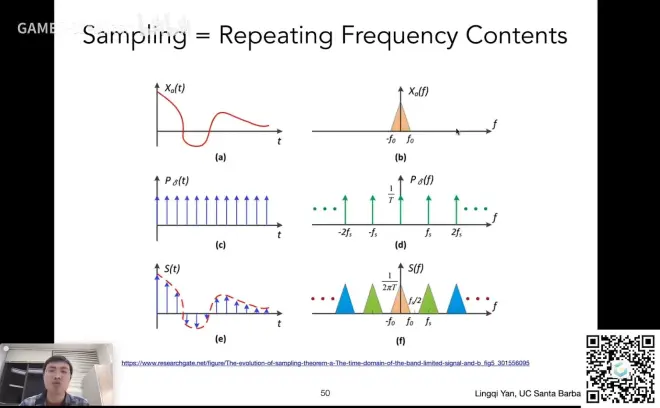
左边一列是时域，右边一列是频域

对a图像进行c的采样，得到e

对应的操作在频域中就是bdf

时域的采样在频域中就就体现为频域信号的复制

（这里老师说左边时域进行乘积=右边频域的卷积，和前文说的不一致，我去查了一下，好像两种说法是相互的，都可以，这里不太懂，但是不影响整体的理解）

为什么会产生走样呢？

采样不同的间隔，会引起频谱不同间隔进行复制，所相交的部分就是走样

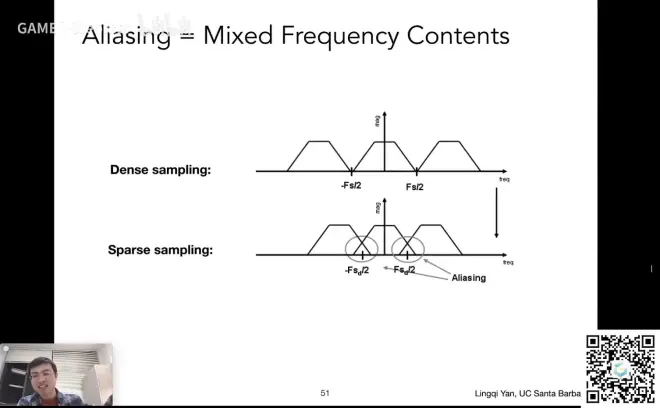
反走样

先对图像做模糊（把高频信息拿掉），再采样

把高频信息砍掉，砍掉虚线方块以外，在以原始采样频率进行采样

这样频域图像就不会发生混叠，也就没有走样了

对覆盖面积求平均，也就是卷积

MSAA（Multisample Anti-Aliasing）多重采样抗锯齿

通过更多的样本来近似三角形的覆盖率，并不是提高采样频率

把一个像素划分为几个小点，判断这些小点是否在三角形内，再把结果平均起来，就知道三角形覆盖了这个像素的百分之多少

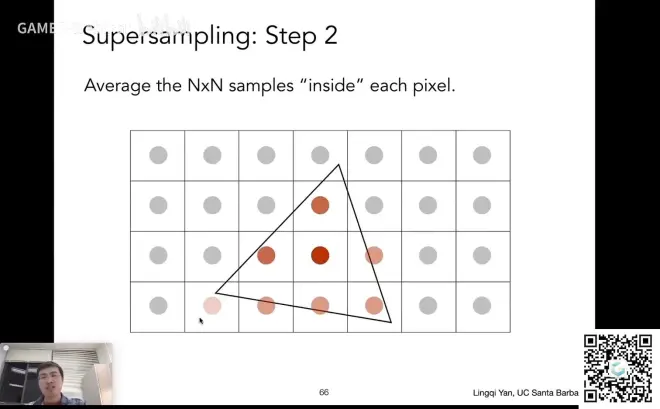
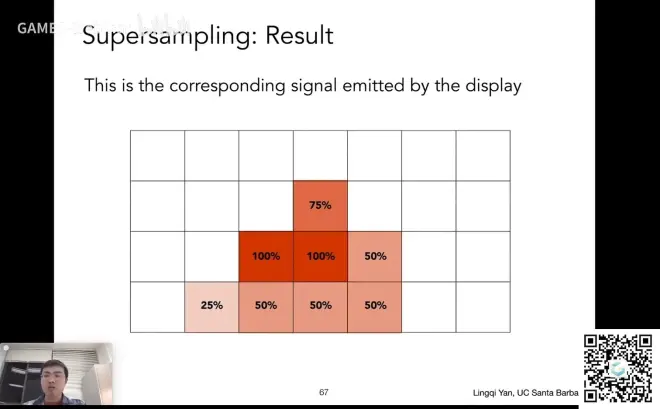
并不是简单的提高了采样的频率，只是用来做第一步模糊，求三角形的覆盖率，平均之后是什么

MSAA解决的其实是对信号的模糊操作

在工业界并不是直接将每个像素平均分了四份，而是采用了一些独特的图形，而且一些边缘的像素还会被复用

关于FXAA可以去看一下Games104，里面讲的比较详细

https://www.bilibili.com/video/BV1kY411P7QM?t=2202.2