本期我们进行运筹学之整数规划的讲解，我们将对割平面法和分支定界法的基础知识进行一个简单的回顾，并介绍求解割平面法的Python相关代码以及分支定界法的MATLAB和Python相关代码，以帮助大家利用工具快速求解整数规划问题，做到事半功倍。话不多说，我们一起来看看吧！

   

一、基础知识

1、整数线性规划的数学模型及解的特点

★ 整数线性规划模型的一般形式

整数线性规划数学模型的一般形式为：

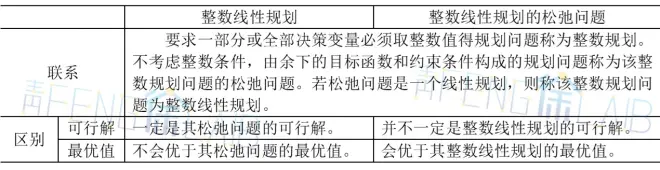
★ 整数线性规划的类型

★ 解的特点

★ 求解方法分类

（1）割平面法—可求纯或混合整数线性规划；

（2）分支定界法—可求纯或混合整数线性规划；

（3）隐枚举法—求解“0-1”整数规划；

（4）匈牙利法—求解指派问题（“0-1”整数规划特殊情形）。

割平面法和分支定界法都是精确算法，在组合优化领域用于寻求最优组合方案，二者利用各自的方法不断增加约束、缩小解空间，再通过单纯形法得出新的解空间下的最优解，最后判断新解是否为整数，不是则继续迭代。本期我们将对割平面法和分支定界法的求解步骤及其算法实现进行介绍。

★ 算法比较

2、割平面法

★ 基本思路

先不考虑整数约束条件，求松弛问题的最优解，如果获得整数最优解，即为所求，运算停止；如果得到的最优解不满足整数约束条件，则在此非整数解的基础上增加新的约束条件重新求解。这个新增加的约束条件的作用就是去切割相应松弛问题的可行域，即割去松弛问题的部分非整数解(包括原已得到的非整数最优解)，而把所有的整数解都保留下来，故称新增加的约束条件为割平面。当经过多次切割后，就会使被切割后保留下来的可行域上有一个坐标均为整数的顶点，它恰好就是所求问题的整数最优解。即切割后所对应的松弛问题，与原整数规划问题具有相同的最优解。

★ 求解流程

3、分支定界法

★ 基本思路

分支定界法是一种搜索与迭代的方法，是在枚举法基础上的改进，其关键是分支和定界。所谓分支，是将非整数值的决策变量分割为与之最接近的两个整数，分列条件，加入原问题中，形成两个后继问题，分别求解，从而把全部可行解空间反复地分割为越来越小的子集；所谓定界，是在分支过程中，若某个后继问题恰巧获得整数规划问题的一个可行解，那么它的目标函数值就是一个界限，可以作为衡量处理其他分支的一个依据。“分支”为整数规划最优解的出现缩减了搜索范围，而“定界”则可以提高搜索的效率。

★ 求解流程

设有最大化的整数规划问题A，它的松弛问题为问题B。从解问题B开始，若其最优解不符合A的整数条件，那么B的最优目标函数必是A的最优目标函数z*的上界，而z的任意可行解的目标函数值将是z的一个下界。分枝定界法就是把B的可行域分成子区域，逐步减小z的上界和增大z的下界，最终求到z*。其求解流程如下：

二、算法实现

1、割平面法

（1）例题介绍

（2）平台实现

我们以上述例题为例，借助Python介绍实现割平面法的相关代码。由于篇幅有限，小编接下来只展示部分代码，小伙伴们可以关注“运筹说”公众号→后台回复“割平面法之Python”获取完整代码。

★ 环境配置

在Python终端输入python -m pip install --upgrade --user ortools后回车，环境配置成功。

★ 代码展示

★ 代码调用

★ 运行结果

最终运行结果展示如下，最优解（x1，x2）=（1，2），max z=1。

2、分支定界法

（1）例题介绍

（2）求解流程

①先不考虑整数限制，解该整数规划问题的松弛问题R0，得最优解为x1=4.81,x2=1.82，可见其不符合整数条件，此时0≤z*≤356；

②因为均为非整数，任选一个进行分支，假设选择x1进行分支，把可行集分成两个子集x1≤[4.81]=4，x1≥[4.81]+1=5，对这两个子集进行规划求解，定界0≤z*≤349；

③对问题再进行分支，得到问题R11和R12，求解后再定界340≤z*≤349，并将R12剪枝；

④对问题再进行分支，得到问题R21和R22，Z22无可行解，于是将R21和R22剪枝，可以断定原问题的最优解为（x1,x2）=(4,2),z=340。

（3）平台实现

我们以上述例题为例，借助MATLAB和Python介绍实现分支定界法的相关代码。由于篇幅有限，小编接下来只展示部分代码，小伙伴们可以关注“运筹说”公众号→后台回复“分支定界法之MATLAB”、“分支定界法之Python”分别获取对应的完整代码。

①MATLAB

★ 代码展示

★ 代码调用及运行结果

回车后得到结果，最优解（x1,x2）=(4,2),z=340。

★ 注意事项

MATLAB只能求解目标函数的最小值，而例题要求目标函数最大值，所以对目标函数进行了乘以-1处理，最后的结果也要乘以-1才是目标函数所求。

② Python

★ 代码展示

★ 代码调用

★ 运行结果

最终运行结果展示如下，最优解（x1,x2）=(4,2),z=340。

三、参考资料

【割平面法Python实现】

https://github.com/xianqiu/opt-alg-tutorials/blob/master/math-prog/int-prog/cutplane.py

【分支定界法MATLAB实现】

https://blog.csdn.net/qq_25990967/article/details/121211474

【分支定界法Python实现】

https://blog.csdn.net/weixin_34162695/article/details/92878875

【分支定界法例题】

https://max.book118.com/html/2017/0905/131924327.shtm

本期的内容就介绍到这里，想要进一步了解运筹学，关注本公众号，快快学起来吧！

作者 | 曹贵玲 尹萌娟 陈梦

责编 | 刘文志

审核 | 徐小峰