小姚老师 | 解析几何“二级结论”（上）

1️⃣直线结论

1. 直线的夹角

• 倒角公式
• 利用直线的方向向量算夹角

2. 直线相关的对称问题

特殊情况：当l的斜率是±1时，可直接由l的方程分别将x，y反解出来，再将点A的坐标分别代入即可求得A'的坐标

倾斜角互补的4种不同说法（斜率和为0）

（1）直线a和a'关于水平线l对称（或者说l为角平分线）

（2）直线a和a'关于竖直线l对称（或者说l为角平分线）

（3）直线α和a'与x轴围出底角在x轴上的等腰三角形

（4）直线α和a'与y轴围出底角在y轴上的等腰三角形

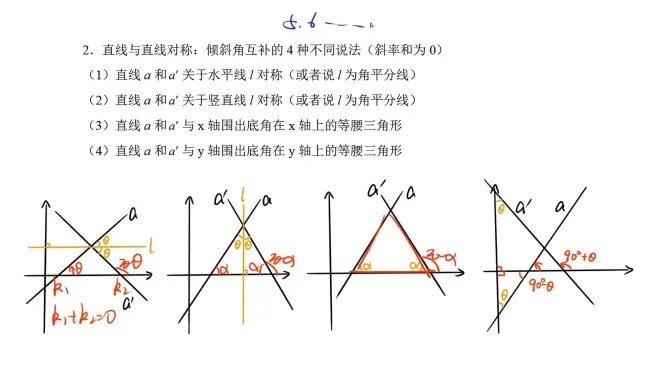
例题1：

角平分线，斜率之和=0

2️⃣圆的二级结论

三角还原：P（x，y）：（α+r·cosθ，b+r·sinθ）

例题2：

三角换元，x=r·cosθ，y=r·sinθ

• 辅助角公式：αsinθ +bcosθ =√α²+b²sin(θ+φ)

定长对定比

AB满足比例式，线段外某点也满足比例式，线段外某点也满足比例式。以这两点为直径所作的圆就是阿氏圆。

设坐标，两点距离公式

3️⃣二次曲线的共有结论

一、改一半法则

1.1 当点P（x₀,y₀）在二次曲线上可改出切线

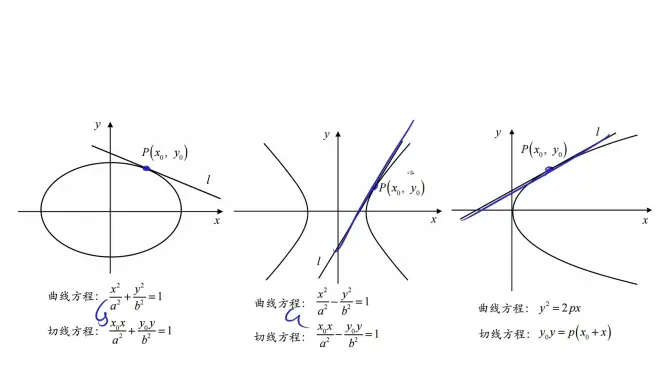
1.2 当点P（x₀,y₀）在二次曲线外可改出切点弦

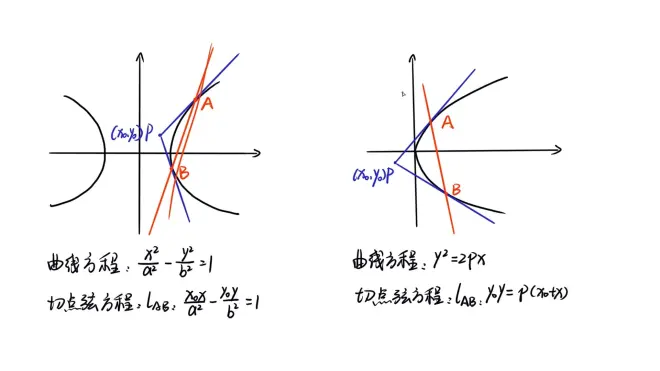
1.3 点在曲线内，改出的直线与曲线相离

二、三大曲线的第二定义

到焦点的距离/到准线的距离 =离心率

三、椭圆双曲焦半径公式

a+e₀ =b² /α-ccosα

例题

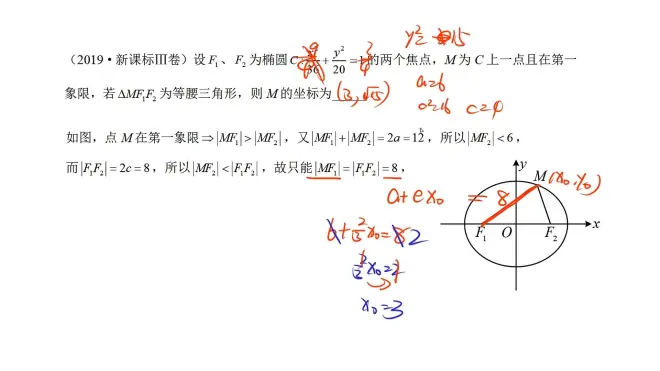
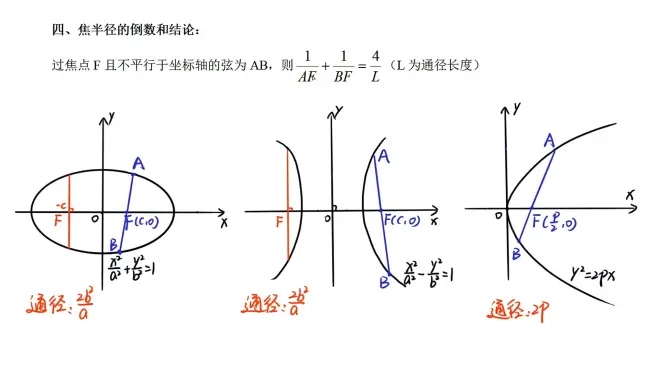
四、焦半径的倒数和结论

1/AF +1/BF =4/L

五、第三定义与点差法斜率积结论

kpa·kpb =-b²/a

例题

渐近线的斜率积结论

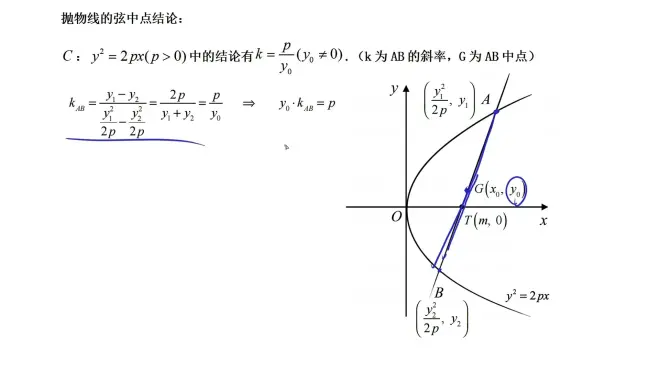
抛物线的弦中点结论

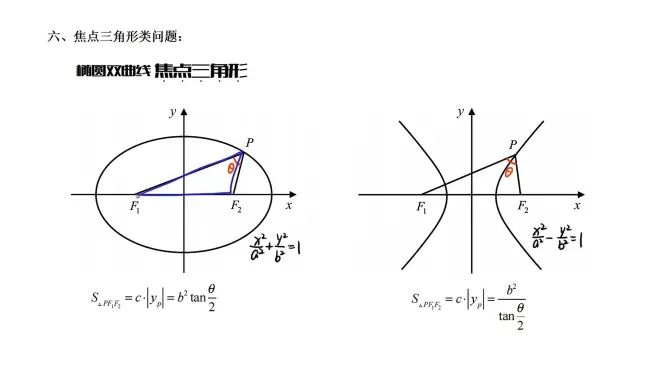
六、焦点三角形类问题

椭圆：c·|yₚ| = b²tanθ/2

双曲线：c·|yₚ| = b²/tanθ/2

例题

七、椭圆、双曲线、抛物线的光学性质

例题