2023数分Day74(含参量正常积分2：积分号下积分法与微分法)

一、整体难度及感受

1、难度上就是要算，必须自己动手算；

2、一些小结论要有意识的记一下；

3、记不住的话得知道是如何推导的.（例如：本节第3题要证的一个定积分，要用到三角函数有理式的不定积分，设u=tan(x/2),则cosx=(1-u^2)/(1+u^2);sinx=2u/(1+u^2),dx=2/(1+u^2)du.这个要知道，不要记错，注意cosx和sinx的分母都是1+u^2，是加法，不要分子分母弄反了，特别是cosx）

二、需要掌握的一些小结论(小结论1-小结论5）

1、含e^x的不定积分（2个）以及定积分（2个，在[0,+∞]上）

2、两个不定积分以及一个定积分的结论

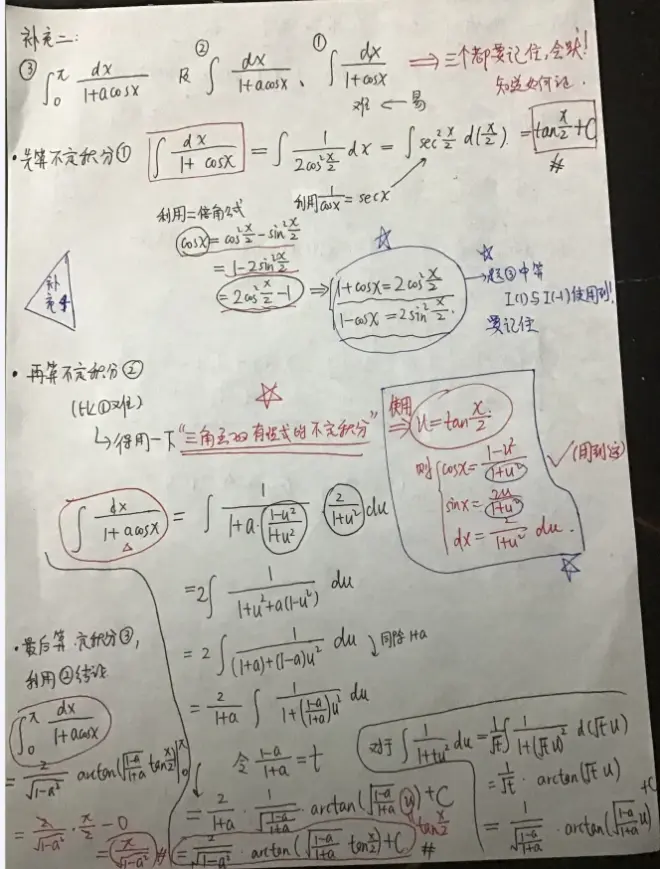
3、升幂降次公式：

对于1+cosx=2[cos(x/2)]^2;1-cosx=2[sin(x/2)]^2，要会变形！

4、三角函数有理式的不定积分（要掌握）

设u=tan(x/2),

则cosx=(1-u^2)/(1+u^2);

sinx=2u/(1+u^2)；

dx=2/(1+u^2)du

5、一个反常积分的结论：ln(sinx)和ln(cosx)在[0,π/2]上的定积分值为-π*ln2/2.（证明使用到了区间再现，今年华东师大定积分考察到，具体习题请参考day28）

三、具体题目

1（郑州大学）

思路：联想到课本原型，本题相当于a取0，b取1.

做法：

先记f(x)，说明其在[0,1]上连续；

然后利用积分可交换次序；

再次验证连续性，说明积分号和极限号可以交换顺序.

复习：课本原型（数分下p184）还是要掌握清楚。

2（暨南大学）

思路：仍然是那个原型。

做法：观察如何找到原函数，再利用夹逼性说明连续性；

接着使用累次积分可以交换顺序；

观察式子，观察到ln(1/x)出现，做一次整体代换，便可以化成含e^x的在[0,+∞]上定积分，这是有公式的，可以直接出来；

最后再算一下一次积分即可。

复习：小结论1

3（同济大学）

考察的小结论很多，这个结论再后续学习中可以用到该结论；而且本题其实是一道课本课后习题。

思路：a范围分成三段，第一段在-1,0,1三点考察，第二段在（-1，1）上考察，最后一段就是剩下情况。

第一段中：计算I(0),I(1),I(-1)(会用到对数函数的一些性质以及小结论3和小结论5）

第二段中：记一下被积函数为f(x,a)；f(x,a),fa(x,a)在[0,π]✖(-1,1)上连续，计算I'(a)（过程涉及凑的技巧以及小结论2，如果小结论2不知道需要会小结论4来推导，注意a范围以及绝对值开出来的正负号问题，不注意可能会出错）,得到导数值为0，说明原函数是常数，再利用(-1,1)上连续，得到了I（a)=I（0）=0，a∈(-1,1)

第三段中：利用第二段结论，有|1/a|<1，0=ln(1/a),代入，利用对数函数性质得到I（a）=2π*ln|a|.

最后总结一下：a∈[-1,1]与其他范围的积分情况即可。