第一性原理计算常见的结果分析
从初始结构出发,多数第一性原理计算软件可以完成电子密度的自洽求解,进一步借助局域优化方法可以得到相对稳定的结构。此时,我们可以通过振动谱、声子谱的计算讨论体现的动力学稳定性,研究体系自由能随温度变化,通过电子结构的计算分析原子之间的成键等。
(1)动力学稳定性和温度效应
以VASP为例,计算振动谱、声子谱在INCAR文件中设置(NSW = 200;IBRION=5;NFREE=2;POTIM=0.02)相关参数,注意参数(案例仅供参考)和版本有关,请大家查找说明书确认。对于团簇、周期结构,如果振动谱、声子谱没有虚频,可以认为体系至少是亚稳态。此外,可以考虑振动熵的贡献,给出体系自由能随温度的变化:

如下图所示,对于总能很接近的同分异构体,考虑了振动熵的贡献后,自由能在700K附近有交点,说明低温下结构I稳定,而高温下结构II相对更稳定。类似的,文献 Phys. Rev. Lett.82, 3500(1999)指出,随着温度的升高,Ag的高指数面(311)将比常见的低指数面(100)和(111)更稳定,和实验结果符合。

(2)原子成键类型和强弱分析
原子聚集后,将出现电荷转移和轨道杂化,我们可以通过差分电荷、PDOS来表征。将体系的电荷减去原子电荷( ICHARG = 12),注意设置两个电荷文件的尺寸要相同(NGXF、NGYF、NGZF),可以看到原子的成键情况。如下图所示,对于给定的硼平面结构(三角晶格和六边形空位组成),把总电荷减去原子电荷,可以看到六边形空位边缘的电荷相对要多一些,对应的键应该也会强一些。

通过PDOS的计算(LORBIT=11),我们可以分辨成键类型,看到成键态和反键态的相对位置,解释结构稳定的原因。如下图所示,CSi中的C和Si轨道对应PDOS有很好的重叠,这是共价键的特征,而CsCl中的Cs和Cl的s和p轨道都是相对分立,表明电荷转移明显,是离子键的特征。文献Phys. Rev. Lett. 100, 206806 (2008)讨论了Ti和Ca在富勒烯表面修饰后对H的吸附作用,H和Ti的配位作用明显,轨道有重叠,而Ca和H的轨道分离,说明是类似静电作用。文献Phys. Rev. Lett. 99,115501(2007)对比了不同结构的硼平面稳定性,发现三角晶格的结构是电子过多,蜂窝结构是电子不足,而三角晶格和六边形空位的组合可以是s+pxy轨道出现带隙,成键态填满,同时没有填到反键态,这样稳定性高。

(3)能带、吸收谱、功函数
完成结构优化后,我们可以固定原子计算电荷密度,然后设置参数(ISMEAR = 0;SIGMA = 0.1;ICHARG = 11)进行能带计算。注意:对于给定结构,可以通过辅助程序得到对应k点的特征线。下图是二维石墨烯的布里渊区和能带。
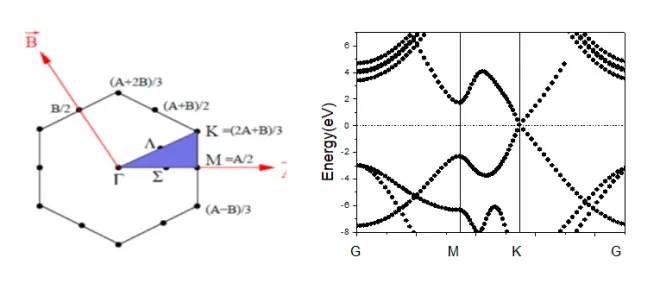
进一步设置参数(LOPTICS = .TRUE.; CSHIFT = 0.1 ),并设置PREC和NBANDS,
可以得到介电函数虚部,和材料的吸收谱可以对应。注意:一般返回的能级数值只有相对意义,所以在画能带时,通常把VBM定成0,对应的是电子的最高能级。如果要计算体系功函数,则需要设置参数(LVTOT = .TRUE. ;LVHAR=.TRUE.),得到体系的电势分布文件,找到真空区域的电势数值,然后和体系费米能级做差即可。
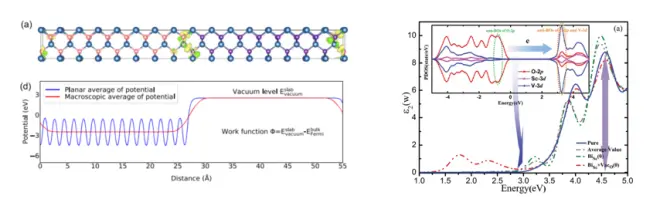
光学性质计算和功函数计算(来自文献: J. Mater. Chem. C,5, 314(2017),Computer Physics Communications 267, 108033 (2021))
(4)特定能级对应电荷分布和STM模拟
为了查看团簇的特定轨道电荷在空间中的分布或者模拟表面结构的STM图像,我们可以设置参数计算得到PARCHG文件。可以指定轨道位置,投影到不同的k点和轨道,设置参数LPARD =.TRUE.;KPUSE=1;LSEPB =.TRUE.;LSEPK =.TRUE.;并通过IBAND指定需要计算的能级。也可以投影到不同的能量区间,设置LPARD =.TRUE.;NBMOD = -2;通过EINT 设置能量区间的左右端点。
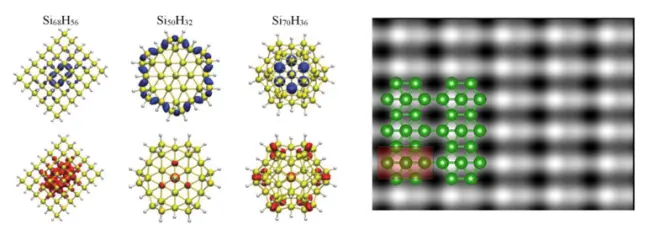
Phys. Rev. B 86, 085440 (2012);Nano Research , 9, 2616(2016))

