利用贝塔函数证明n维球的超体积

在上高中的时候，我们都在数学书上学过利用祖暅原理证明球的体积，然而这种方法的弊端便是构造起来并不容易，并且很难推广到任意维度的情况下。

于是我们有了积分的知识以后，通过积分我们就可以比较轻松地得到三维球体积表达式：

再探索四维球体的体积时我们也可以用类似的方法得到其体积公式：

为什么系数含有圆周率的平方？对更高维的球又应该是什么样的？这篇文章的目标就是用欧拉积分简洁易懂地证明任意维度情况球的体积公式。

这次的专栏一半也是因为3B1B的视频后留的“小作业”，不过这个证明并不需要用到正态曲线的相关知识。

一、建立表面积与体积的关系

首先，我们观察两组式子：

这里，我们把二维球视为圆，二维球的体积视为其面积，二维球表面积视为其周长。

通过观察我们发现，对于二维和三维的球，表面积均为体积关于半径的导数。

我们首先考虑一个圆，将其分割为多个小圆环，并让每个圆环的宽趋向于0，如图：

我们假设圆的“表面积”（为了统一起来，就都这么表述了）为，则圆环面积为，由此我们对圆环面积从0到R（被分割圆的半径）上求和：

反过来，自然有：

而这个规律也可以推广到任意维度的球，如三维球便可以分割为多个同心球壳。四维球？虽然我们不知道它的样子，但因为球的性质，我们仍可以把其分解为多个同心四位球壳......

二、尝试求解三维球与四维球的体积

这里我们先借用一下3B1B视频中分割正态曲面的方法：

在这里，我们将看作一个整体，记为r，并将这个图形分解成了多个空心圆柱的体积之和，通过求和得到了其体积。

类似地，我们也可以将球体体积分为多个空心圆柱体积之和，我们仍令：

类似地，圆柱的宽记为dr，根据球体对应的二元函数解析式，我们得到积分：

这里R指球体的半径，由于r的范围是从0到R，故积分的上下限便可以确定，通过这个积分，我们很容易可以解得（直接凑微分就行）：

对应表面积(体积的导数)：

同理，我们也可以将四位球体分为许多空心球柱（暂且这么叫着），类似地我们发挥推理的的力，原来圆的周长就变为了球的表面积，于是我们也可以写出积分：

这里运用三角换元来求出这个积分的解，最后结果就是我们前文所说的

对应表面积：

这样，我们就已经写出了三维及四维球体的体积与表面积表达式。

三、推广到任意维度的情况

为了方便表述，我们先定义几个符号：

：n维球体积

：n维球表面积

：n维球表面积系数

对系数，我们可以定义为：

首先我们设，根据刚才的推理，我们可以得到通解：

经过变换，由于为常数，因此可以直接扔到外面去，于是：

单独考虑积分内部的东西：

三角换元(这里令r=Rsinx)：

我们注意到贝塔函数的三角形式：

因此

推得：

这里考虑到n与n-3的奇偶性不同，因此我们把奇数与偶数分开讨论

（以下式子默认n≥3）

因此：

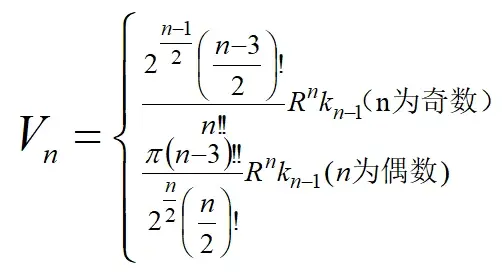
对其求导：

因此我们可以分离出系数：

因此我们再设一个函数：

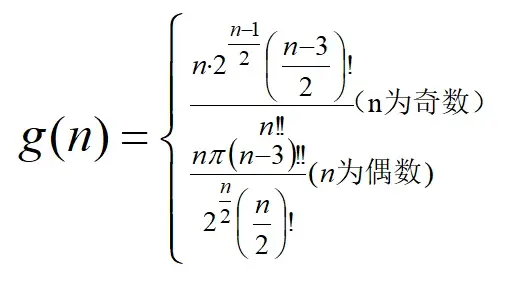
因此对数列，我们有：

由圆的周长可以得到：

因此

整理得（这一步就是分奇偶两种情况写出来，然后可以进行约分，有时间的自己可以算算...）

逆推回表面积：

积分得到体积：

整理合并合并得到最终结果：

四？？？

根据这个结论，我们可以得到一些有意思的东西：

-1维球体积随半径的增大而减小，表面积是负值，绝对值也随半径的增大而减小。

这个规律对于-1，-5，-9......维的球是成立的

但是对于其他负奇数便是另一种情况，拿-3维为例：

其体积是负值，表面积是正直，且二者的绝对值均随半径的增大而减小。

而对于所有负偶数，其表面积体积都趋于0......

并且如果可以计算的话，你可以求出任何一个维度（除了负偶数）下的球体体积与表面积，e维，π维，甚至是i维！

这大概是相当于一个解析延拓的效果？？？

最后，也感谢3B1B为我提供的新思路（这里附上原视频地址）

如果存在错误，请指出，不胜感谢！