这个看似抽象的数学问题，其实能拯救你的生命

数学作为隐喻的一个主题

The Single Motif of Mathematics as Metaphor

图壹

所有几何体（柏拉图式/欧几和非柏拉图式/非欧几）的潜在化身是什么？

换句话说,在正曲面和负曲面上产生的所有形态的单一主题是什么？

What is the underlying avatar of both Platonian/ Euclidean and Non-Platonian/ Non-Euclidean geometry?

In another word, what is the single motif of both positive and negative curvature?

图贰

我们先来了解一下多项式，它有一些根，【以希腊和中国阴阳之五行为例有 5 个-- 图叁，柯蒂斯 · 麦克马伦教授的所居的例子有 4 个 - a,b,c,d-- 图伍】根可以被认为是有着一定股数的辫子/结，而值得注意的是，辫子/结产生的形态与面不仅仅是柏拉图/欧几几何体（图叁），同时也可以是非柏拉图/非欧几几何体 （图肆）

A polynomials with some roots to be thought of as strands of a braid, the resulting shape and associated surface yield both Platonic and Non-Platonic Geometry（examples were given first with both classical Greek and Chinese Five Elements as 5 roots, and the immediate example following provided by Professor Curtis McMullen with 4 roots.）

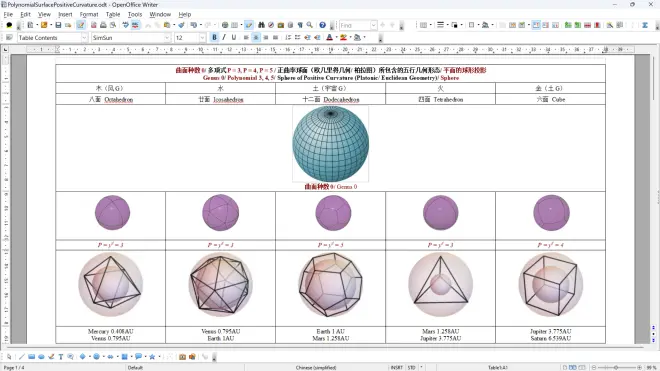
图叁 柏拉图/欧几几何体

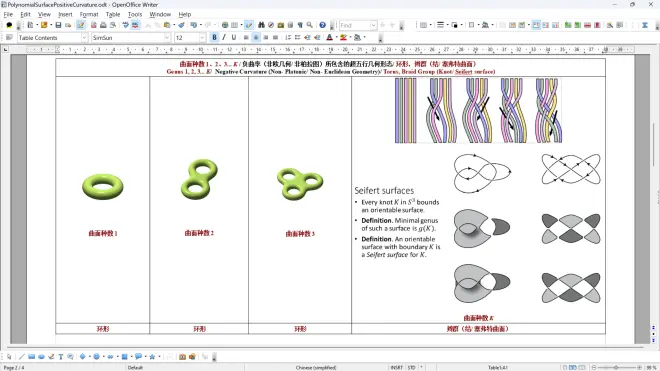
图肆 非柏拉图/非欧几几何体

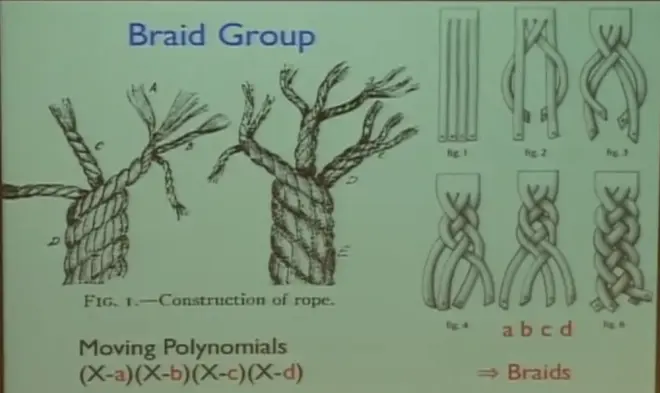
图五 柯蒂斯 · 麦克马伦教授的例子

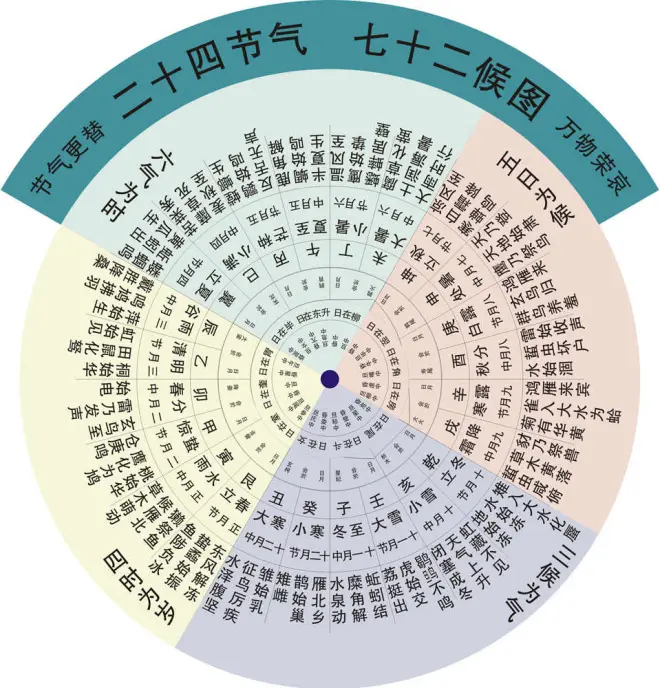
接下来我们看波斯（现伊朗）拜火教和中国传统宇宙观的数学隐喻，包括 3 个穗组，每组 24 根线，总共产生 72 股 （图柒）

Let's investigate the cosmological metaphor expressed with numbers/ Mathematics by not only Zoroastrian and Chinese, but also by Indian Jainism as well as presented in Solomon's Goetia.

图陆

图柒

那么回到主题，每组 24 根线，总共产生 72 股作为数学隐喻的一个主题究竟是什么？我们让中国传统历法来揭开它神秘的面纱。

世界其它文化中的源代码

印度耆那教

24位寻路者

所罗门王的的72灵

更深的意义请参考以下视频：

【源代码】

https://www.bilibili.com/video/BV1d44y1F71M