By: Tao Steven Zheng (郑涛)

【Problem】

 Jiuzhang Suanshu (Gougu 16)

Suppose there is a right triangle whose gou (shorter leg) is 8 bu, and gu (longer leg) is 15 bu. What is the diameter of the inscribed circle?

【Solution】

Let  be the side lengths of the right triangle, where  is the hypotenuse. Let  be the radius and  be the diameter of the inscribed circle. Dissect the right triangle into 6 pieces (Figure 1): 2 red triangles, 2 blue triangles, and 2 yellow triangles.

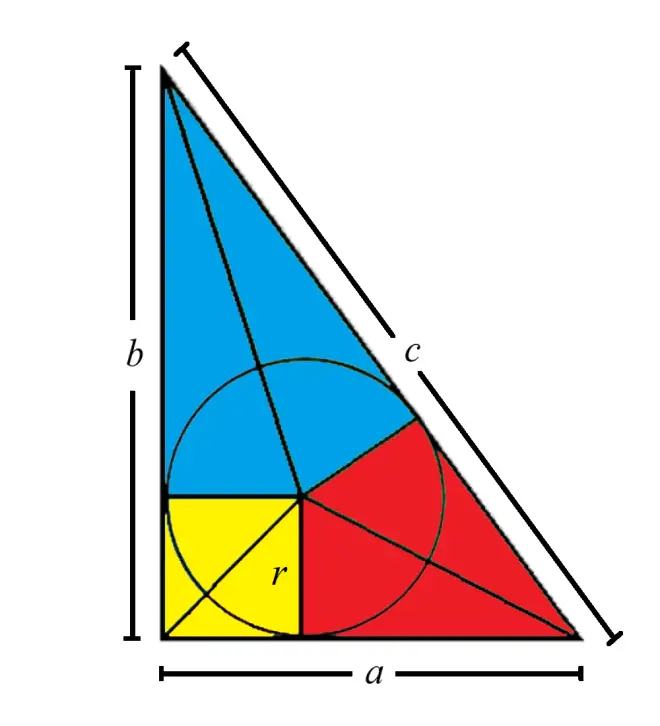
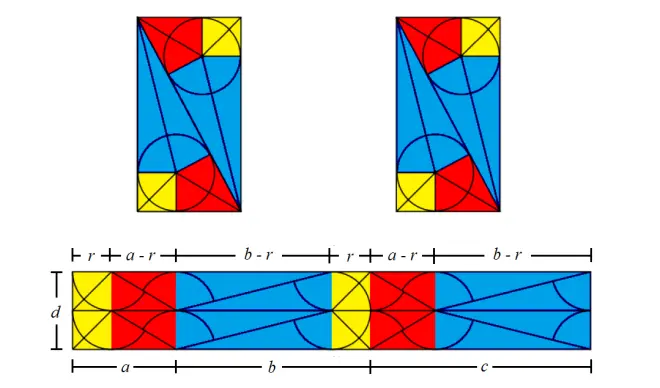
Copy each rectangle four times (Figure 2 top), then combine each pair of triangles of the same color to form rectangles (the yellow triangles form a square). Assemble them to form one large rectangle (Figure 2 bottom). Use this large rectangle to derive three different formulas for calculating the diameter of the inscribed circle.

Formula 1

The area of a large rectangle is equal to the area of four right triangles:

Formula 2

It can be seen immediately from (Figure 2 bottom) that:

It is known that and , thus

Formula 1

Formula 2

Therefore, the diameter of the inscribed circle is 6 bu.