Practice_1_a difficult limit exercise

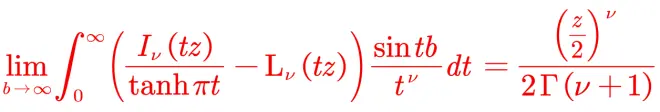
Where  is modified bessel function of the first kind

 is modified struve function

Before tackle this limit, I mention a lemma which would be used in procedure.

Lemma:

above formula holds when 

But according to the theorem of analytic continuation, the limitation  can be deleted.

Proof of Lemma:

Denote 

Expand   to series and exchange the order of the double summation

The sum of the nested series had been evaluated earlier

(its proof won't be posted here because of its cumbersome process, but I will prove it in my next article)

Its value is given by

 

which holds when

Plug its value into , we obtain

Exchange the order of the former summation, and note that the latter series is modified Struve function of order .

Hence,

To calculate the former series, replace  by , hence

Obviously, the double series is the product of two simple series

where

and

Plug these value into , and after some elementary operation, we obtain

Then we can calculate the limit  by using the lemma which is proved earlier in this article.

On the one hand

multiply both sides by , and integrate  from 0 to infinity, we get

On the other hand, according to the integral expression of Bessel function of the first kind

exchange the order of integration and summation

Note that the two integral 

and 

are both derived from the series 

Hence

Take the limit both side as  tend to infinity.

At last, replace  by , we obtain