《超弦和M理论导论》1.2

1.2 规范理论的历史回顾

在二十世纪六十年代，基本粒子物理似乎陷入困顿的绝境中了。弱、电磁、强和引力彼此分开进行研究，将彼此拉开了非常远的距离。此外，对各种力的研究已经碰到了一块基本的路障：

（1）弱相互作用。（The weak interactions.）弱相互作用的理论模型已经尴尬地在三十年前的二十世纪三十年代费米（Fermi）理论首次提出后有了小小的进展：

Γ上标A代表了狄拉克（Dirac）矩阵多样的组合。接下来的主要步骤，一个W玻色子的理论，因为无穷的问题而相当令人苦恼。还有，没有人知道轻子背后的对称，或者不知道是否会有这种对称。

（2）强相互作用。（The strong interactions.）与弱相互作用相比，汤川（Yukawa）介子理论给出了一个强相互作用的可重整化理论：

————

8

然而，汤川理论不能解释在粒子加速器中“基本”粒子雪崩式的发现。尤利乌斯·罗伯特·奥本海默（J.Robot Oppenheimer）甚至建议那一年的诺贝尔物理奖不应该颁发给没有（didn't）发现新粒子的物理学家。此外，夸克模型——似乎与数据吻合得比它能做到的还要好，也很惘然于夸克从没在实验中被观测到的事实。

（3）引力。（The gravitational force.）引力的研究完全和其它作用力分开了。经典相对论家持续着孤立地在粒子研究中寻找更多经典解决方案。教条式量子化该理论的尝试被该理论巨量赘余的出现给搞迷糊了。人们还沮丧地认识到即使该理论可以成功量子化，它也不是可重整化的。

这片荒凉的景象在二十世纪七十年代规范革命的到来中产生了戏剧性变化。自旋1规范粒子的完全可重整化理论的发展成为了过去25年的伟大成就之一，这样物理学家们终于可以第一次计算真正的S矩阵元素了。因此，对麦克斯韦在十九世纪六十年代首次提出的最初的规范理论的超越花了100多年！（参见附录上对规范理论和群论的基本介绍。）

显然消除相对论量子力学的发散的关键在于寻求更大更精密的规范群。对称现在成为粒子模型最重要的特征，而不是纯粹艺术上的特征。

例如麦克斯韦方程组第一次统一电与磁力使用的是U(1)的规范群。弱力和电磁力的弱电统一需要SU(2)⨂U(1)。使夸克粘合在一起成为强子的力，或量子色动力（QCD）基于SU(3)。所有基本粒子物理实际上和SU(3)⨂SU(2)⨂U(1)最小化理论是一致的。

尽管大统一理论还没有能统一弱力和强力的定论，它的统一主题也同样也是规范理论，使用了诸如SU(5)、O(10)等对称。

尽管规范革命可能是几十年来最重要的进展之一，也还不够。科学家们逐渐意识到杨-米尔斯理论自身不能推进我们超过现在水平的物理宇宙的理解。大统一理论不仅无法解释重要的物理现象，在阐述量子引力理论方面也有非常大的问题。

大统一理论首先不能成为所有力统一的最后一个词句。有一些大统一理论仍然没有解决的点：

————

9

（1）大统一理论不能解决为什么有三种几乎相同的基本粒子家族。我们仍然无法回答拉比（Rabi）的问题：“谁创造了μ子？”

（2）大统一理论仍然有20个左右的任意参数。这些参数，比如说，不能计算夸克的质量或是多样汤川耦合。一个真正的统一理论应该只有至多一个任意参数。

（3）大统一理论对解决分级问题有困难。除非使用超对称，否则很难阻止大量粒子物理与宏观能量搞混并破坏其层次结构。

（4）粒子力在大约10^-28厘米的地方统一，很接近10^-33厘米普朗克（Planck）长度，我们猜测在这里引力的效果会占支配地位。但是大统一理论没有提到任何有关引力的东西。

（5）至今，质子衰变还没确定被观测到，这已经排除了SU(5)的最小化。因此，还没有令人信服的实验证据来推广此理论。

（6）要我们相信当今的能量和统一量度中没有新作用力是很难的。“荒漠”很可能会在未知新作用力中喷发。

从根本上来讲，这些问题中最复杂也是最有挑战性的是寻找到一条量子化爱因斯坦广义相对论的道路。尽管杨-米尔斯理论已经取得了统一已知粒子物理定律的巨大成功，但是引力定律在底层上特别不一样。显然，杨-米尔斯理论和传统规范理论处理此问题时无能为力。因此，大统一理论当被推及他们的极限时便面临着可怕的实验性和理论性问题。

广义相对论在推及它的极限时也被相似的困难所困扰：

（1）传统上，我们已经确定爱因斯坦方程必然表现出点状奇点，在这里我们推测广义相对论的定律会崩塌。在此领域量子修正必须夺去经典理论的宝座。

（2）作用量并非从下约束的，因为在曲率张量中它是线性的。因此，量子力学上的作用量可能是不稳定的。

（3）广义相对论不可重整化。譬如计算机计算确定显示在双环水平上爱因斯坦理论里有一个非零的抵消项。

量子化爱因斯坦重力理论的天真尝试已经遭遇了令人沮丧的失败。第一个首先指出广义相对论和量子力学不兼容的人是海森堡，他指出一个量纲耦合常数的出现会毁灭正常的重整化进程。

————

10

如果我们设：

这里甚至还留下一个牛顿引力理论上的量纲常数——引力常数G：

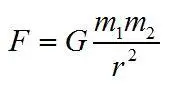
该常数有厘米平方的量纲。当我们用度规η下标μν=（- + + +）把度规张量g下标μν围绕平方幂展开，我们就引入了耦合常数κ，该常数有厘米的量纲：

因此

在此单位系统中，唯一的单位是厘米，该耦合常数κ变成了普朗克长度——10^-33厘米或者10^19千兆电子伏特，那远远超出了实验所及的程度!

然而重整化理论是在我们可以用一个对无限再定义某些常数消除所有发散的基础前提上建立的。有一个负的量纲耦合常数意味着这种图像复杂的洗牌和恢复是不可能的。负的耦合常数意味着我们一直都可以在费曼图中插入一个作用形式并增强它的发散幂级数。这代表着任何一张图都可以通过大量插入做到任意的发散。这意味着广义相对论不会是一个可重整化的理论。（This means that general relativity cannot be a renormalizable theory.）例如引力子-引力子散射的振幅现在就变成了一个单量纲参数的幂展开（参见图1.3）：

这样我们再也不能用通常的方式给图洗牌来消除无穷了，这本该是重整化理论的心脏。因此，重整化理论破产。

因为广义相对论距离重整化理论管的地方太远了，所以我们必须重新考虑狄拉克根本的反对意见。狄拉克说量子力学的成功是基于在其中各种修正项都越来越小的近似方案。但是重整化理论因为其触犯该原则、修改无穷量并在最后消去了它们，而是残缺的。

一个解决方案是建立一个对于耦合常数中的每个都是有限的引力理论，这样就再也不需要重整化理论了。有一段时间，大有希望的是超重力，它是基于局部规范

————

11

群Osp(N/4)（参见附录），这个群是爱因斯坦方程在60年间第一个非平凡延展。希望就是该规范群可能给我们一套足够大的沃德-高桥（Ward-Takahashi）恒等式消除一大批发散图像。规范群越大，恶心人的无穷越能够消除。（参见图1.4）：

正在努力实现的基本对策是：

规范对称→沃德-高桥恒等式

→图像的消去→重整化理论。

比如说，爱因斯坦的引力理论都要在单环水平上显示出平凡的有限。有一个出彩的等式叫做高斯-波内特（Gauss-Bonnet）恒等式，它直接展示所有广义相对论的单环图（这可能要一台计算机才能画下来）的总和是零。实际上，超高斯-波内特恒等式消除了超引力诸多的发散，但很可能不足以让理论有限化。

最大号也是最有戏的超引力，O(8)超引力很可能是发散的。不幸的是，我们有可能在第七环水平上写出局部超对称抵消项。如果不引入一个更大号的对称，那要全部消除该项系数和可能是其他抵消项的无穷大数是很不可能的了。这令人

————

12

沮丧，因为这意味着最大号超引力理论的规范群Osp(8/4)对消除广义相对论发散来说还是太小了。

以及，O(8)规范群要容纳SU(3)⨂SU(2)⨂U(1)最小化粒子物理也还是太小了。如果我们采用比O(8)还要大的群，我们就会发现我们必须将越来越高的自旋数塞进该理论中。然而，自旋数为3的相互作用理论很可能不存在，这让我们怀疑O(8)就是一个限制超引力理论的群。

总之，超引力有这两个根本原因必须被剔除了：

（1）它很可能不是有限理论，因为规范群的大小不足以消除所有可能的超对称抵消项。因此在第七环的水平上有一个可能得无穷大抵消项。

（2）它的规范群O(8)还没大到可以容纳粒子物理的最小化对称，也就是SU(3)⨂SU(2)⨂U(1)，它也不能容纳手性费米子。

物理学家们面对这些以及其它的障碍有好几年了，他们总结出也许我们所认定的宇宙假设必须有一个或者几个需要抛弃掉，因为广义相对论和量子力学可能是从一个小公设上发生分歧，这些公设中的一个或者几个必定是错误的。关键是必须丢弃我们用以建立广义相对论和量子力学的自然常理中的一个。多年来，为了抛弃我们有关宇宙的部分常识概念，已经有了几个建议：

（1）连续性

这一方法假设时空必须是粒状的。这些粒子的尺寸可能得到费曼图的自然中断，允许

————

13

我们得出有限S矩阵。像是

这样的积分会像ε^-n一样发散，但我们永远不会在ε为零时接受这个极限。格引力理论就是这一类。比如在雷格（Regge）运算中，我们用离散的四个单形格化雷曼空间，并用沿单形画圈圈时计算的角亏损来代替曲率张量：

（平滑空间上，围绕闭合路径没有角亏损，这个作用量就跌落了。）通常来讲，在格的理论中，我们当格长取零时取极限。但是这里我们把它固定成一个小量。然而现在，没有实验证据表明时空是粒状的。尽管我们永远不能剔除这一方法的猜想，这似乎违背了粒子物理学的自然发展规律，而规律已经是以更大号和更优雅的群为公设。

（2）因果律

这一方法允许我们小小地违背因果律。包含李-维克（Lee-Wick）力学的理论事实上是可重整化的，但是允许在因果律上有小偏差。这些理论通过虚构质量M的泡利-维拉斯（Pauli-Villars）场来改变传播子的紫外行为使得费曼图收敛。通常在紫外极限下，费曼传播子收敛为p^-2。然而在添加一个虚构粒子后，我们甚至可以让传播子收敛得更快，像是p^-4：

注意到泡利-维拉斯场是鬼场，因为传播子中出现了-1（这代表该理论会充满负的概率）。通常我们让泡利-维拉斯场的质量趋于无穷。然而这里我们让它变成有限值，让这一极伸到非物理的薄板上。然而对结果费曼图的结构的考察表明，因果律被违反了；也就是说你可以看见你出生前的父母。

（3）统一性

我们可以替换爱因斯坦的理论，该理论是基于曲率张量的，就用一个基于外尔（Weyl）张量的共形理论来代替：

————

14

当外尔张量定义为

这里的括号代表反对称化。该共形张量拥有比曲率张量更大的对称群，也就是，局部共形变换背后的不变性：

外尔理论是收敛的，因为传播子是p^-4，即它是个高度可微的理论。然而因为上面说的原因，有一个“统一幽灵”也在传播子中与a-1一起出现。最乐观的设想是叫一个类似于夸克禁闭的力学让这些统一幽灵“关禁闭”。

（4）局部性

多少年来也有了主张丢掉量子力学一些重要假设，比如局部性的建议。毕竟，没有保障说量子力学的定律能在10^-33厘米处还成立。然而物理学家每每试图去偏离量子力学的定律如因果律时，都总会出一些问题。现在还没有成功的量子力学替代品。

（5）点粒子

最后是超弦一派，它抛弃了理想化点粒子的概念，这个概念是希腊人在2000年前提出的。

超弦理论因其只丢掉了物质的基本成分必须是点粒子的假设，也就对我们持守的物理原则破坏得最少，并延续增加规范群复杂性和精密性的传统。超弦理论并不违反量子力学的任何定律，但做到消除大部分——如果不是全部，费曼图的发散。超弦模型的对称群是物理史上见过的最大群，很可能足够大到让理论在任何情况下都是有限的。再说一遍，它的对称性，而不是量子力学的崩溃，是使理论有限的根本关键。

在图1.5中我们戏剧性地看到不同引力理论的演变。首先是牛顿（Newton）理论里的超距作用，这里引力作用跑得比光还快，爱因斯坦用曲面流形的经典演绎替代了它，量子引力相应地通过增加环给爱因斯坦的理论做量子修正，最后超弦理论通过加和所有可能的作用弦拓扑构造对点粒子量子理论做出进一步修正。

————

15

然而超弦理论和它的历史发展中的前辈相当不同。不像是其他物理理论，超弦理论拥有或许是科学史上最奇怪的历史之一的历史，这段历史有着比过山车还多的弯弯。

首先，两位年轻科学家威尼斯诺和铃木在他们翻阅一本数学书并惊奇地注意到欧拉贝塔函数满足S矩阵强子作用的所有假设（除了统一性）时独立发现了它的量子理论。内弗（Neveu）、施瓦茨（Schwarz）和雷蒙德（Ramond）很快就将理论推广到包括自旋粒子的领域。为了解决统一的问题，吉川（Kikkawa）、铃木和维拉索罗（Virasoro）提出欧拉贝塔函数应该看作是一个微扰级数的玻恩（Born）项。最后，加来、郁（Yu）、洛夫莱斯（Lovelace）和亚历山德里尼（Alessandrini）通过计算玻色子的多换图完成量子理论了。然而该理论仍然完全是以在壳S矩阵振幅的形式阐述的。

随后，南部（Nambu）和后藤（Goto）意识到潜伏在这些散射振幅后面的是一个经典的相对论弦。霎时他们就通过揭露理论背后统一和经典的图像改良了整个理论。经典理论和量子理论的关系很快就由戈德斯通（Goldstone）、戈达德（Goddard）、雷比（Rebbi）和索恩（Thorn）建立起来并由曼德尔施塔姆（Mandelstam）推广。但是该理论仍然是作为

————

16

半经典量子化被阐述的，从而必须临时假定量度、顶点、图像数目等东西并且不能从半经典原则中演绎出来。

加来和吉川最后写出了作用量（在特殊的规范中），最后，这个模型可以严格地以物理变量的形式从一个作用量中推出，尽管作用量没有剩下任何对称了。然而，当发现该理论只在10维和26维有定义时，该模型很快就死亡了。此外，作为强子作用的理论，量子色动力学的飞快发展似乎给超弦的棺材板钉上最后一根钉子了。

十年来，因为没有人相信一个10或26维的理论和四维物理间有什么关系，所以这个模型一直半死不活。当舍尔克（Scherk）和施瓦茨做出了该对偶模型实际上是一个所有位置作用力的模型的骇人猜想时，没人把它当回事。这个想法像铅气球一样落下了。

1984年格林（Green）和施瓦茨发现超弦理论没有任何异常而且很可能在微扰理论中对任何情况都是有限的，他们便复活了这个理论。E8⨂E8高斯、哈维（Harvey）、马丁内茨（Martinec）和罗姆（Rohm）“杂化弦”被认为是统一引力和粒子作用物理合理模型的最佳候选。

现在有个很火的的研究领域是完成该理论的演化，发现为什么模型中有这么多“奇迹”。已经有了一系列朝向使用中间10年发现的方法给出协变作用量的活动，比如BRST。

最后，二十世纪九十年代初对对偶集中的研究，特别是1995年威滕（Witten）和汤森德（Townsend）的工作，确立了M理论作为弦理论最新、最高等的阐述。现在这五种超弦理论可以在11维上统一为一个单一的理论，也许是在膜的层面上。此外，低维中对偶关系的巨大网络为我们提供了探索弦理论非微扰解的“路线图”。然而，我们缺少的还是理论最终依托的几何。理解了这种几何结构，我们就可以把整个理论表述成一个简单、连贯的方程。这样就可以完成这一理论的演化，而在过去的30年该理论一直在逆向演化。

量子理论→经典理论→作用量→几何

让我们总结一些超弦理论有望成功的正面特征：

（1）规范群包含比SU(3)⨂SU(2)⨂U(1)最小化群大得多的E8⨂E8。该理论有足够的空间来容纳现象。

（2）该理论没有异常。这些量子场论小但是重要的缺陷对诸多自洽理论类型

————

17

给出限制。超弦理论的对称性通过一系列的“奇迹”消灭它所有可能的异常。

（3）黎曼曲面理论的有力论证表明该理论是在任何微扰理论中都有限的。（尽管缺乏严格证明）

（4）有很少的自由性。众所周知，要在不破坏其神奇特性的情况下修补超弦模型是非常困难的。因此，我们不存在19个任意常数的问题。

（5）该理论包含大统一理论、超杨-米尔斯理论、超引力理论和卡鲁扎-克莱因（Kaluza-Klein）理论等子集。因此，为这些理论化发展起来的现象学的许多特征延续到弦理论中。

粗略地说，超弦理论将各种力和粒子结合起来，就像小提琴弦提供了音乐音调的统一描述一样。就其本身而言，音符A、B、C等并不是最根本的。然而，小提琴的琴弦是基本音；一个物理对象可以解释音符的多样性甚至是我们可以从中构建的和声。同样的，超弦提供对基本粒子和力的统一描述。事实上，超弦创造的“音乐”就是自然界的力和粒子。

虽然超弦理论由于其一套庞大得令人难以置信的对称而“奇迹般地”消除异常和发散，但我们也必须一碗水端平，指出它的不足之处。为了公平起见，我们还必须列出该理论的潜在问题，这些问题已经被模型的批评者指出来了：

（1）在实验中不可能达到在普朗克尺度上发掘的巨大能量，因此该理论在某种意义上是不能检验的。一个不能检验的理论也是不能被接受的物理理论。

（2）还没有发现一丝实验证据确定超对称的存在，更别说超弦了。

（3）假设在100到10^19千兆电子伏特之间的“荒漠”中不会出点差池也太放肆了。当我们增加加速器的能量量度时，总是会出现全新的、完全出乎意料的现象。然而超弦理论预测了接下来的17个数量级，这在科学史上闻所未闻。

（4）该理论没有解释宇宙常数为什么为零。任何声称自己是“万有理论”的理论肯定都要解释消失的宇宙常数之谜，但超弦该如何解决这个问题目前还不清楚。

（5）这个理论的丰富性也很尴尬。显然有数百万种方法可以把这个理论分解成低能状态，那么哪个才是真真空？虽然超弦理论可以得出SU(3)⨂SU(2)⨂U(1)最小化理论，但它也预测了许多其它尚未被发现的相互作用。

————

18

（6）没有人真的知道如何把一个10维理论分解成四维。

对该模型的六种反对意见中，最根本的是最后一种，即无法计算出维度的分裂。理由很简单：微扰理论的所有情况中，时空维数都是稳定的。因此为了让理论自发地卷曲成四维和六维宇宙，我们必须求助于非微扰的动力学效应，而这是出了名的难以计算，这就是寻找理论背后的几何如此重要的原因。模型的几何公式可能会提供给我们模型的关键理解，这将使我们能够进行非微扰计算，并用理论做出明确的预测。

因此，关于该模型不能在普朗克长度上进行测试的批评实际上有点欺骗性。如果超弦理论能够成功在动态上分裂，它也应该能够向下做出精确到宏观能量水平的预测。（The superstring theory,if it could be successfully broken dynamically,should be able to make predictions down to the level of everyday energies.）例如，它应该能够预测夸克的质量。因此，我们不必再等几个世纪就能拥有达到普朗克长度的加速器。

因此，超弦理论面临的根本问题不非得是实验问题，它主要是理论上的。该理论的突出问题是计算动态对称性破缺，使其在普通能量下将预测和实验数据进行比较。（Thus,the fundamental problem facing superstrings is not necessarily an experimental one.It is mainly theoretical.The outstanding problem of the theory is to calculate dynamical symmetry breaking,so that its predictions can be compared with experimental data at ordinary energies.）

普朗克能量下的基本理论也是普通能量下的基本理论。因此，理论发展的主要绊脚石是对其非微扰行为的理解。

然而在书本第1部分中我们将遵循历史先例，提出该模型的半经典量子化阐述。正如我们要在本书中强调的那样，半经典量子化理论似乎是随机事实的松散组合。因此我们已经强调路径积分公式（是首先由薛（Hsue）、文二和维拉索罗为了威尼斯诺模型所写）作为阐述半经典量子化理论的最有力方法。尽管路径积分方法无法揭示模型的底层几何公式，但它提供半经典量子化理论最全面的阐述。

我们不会去找点粒子理论的泛函公式，因为它几乎可以直接纳入弦理论。

————