大学物理(光学)知识梳理与例题选讲:§01 光学基础知识

光的产生与光的性质
所用教材为:赵凯华《新概念物理教程(光学)》高等教育出版社.2004

# 光学基础知识
## 光的产生与光的性质
### 产生原因
- 电致发光:电路当中发出的光
- 化学发光:如:物质的燃烧,化学反应中释放能量,其中产物以光的形式释放
- 光致发光:主要指荧光
- 生物发光:生物体发出的光,其为冷光,无热效应
光源:发光物体
### 光的本质
- 光是一种电磁波
- 光是一种粒子
### 光的描述方程
平面电磁波的方程
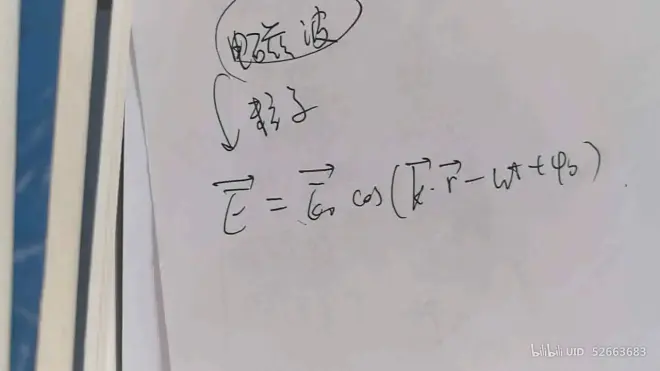
方程形式的解释:
#### 波动方程的解释——波矢k

梯度ΔE

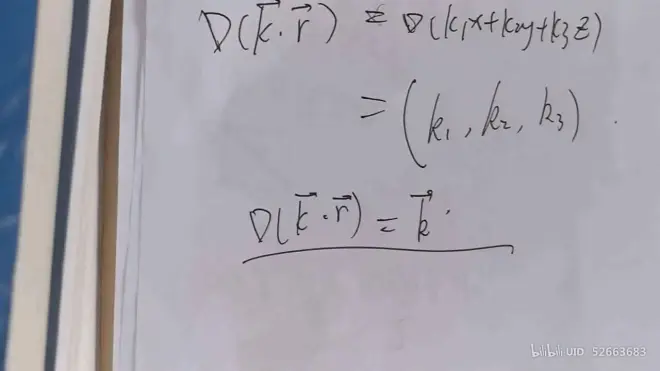
#### 波动方程的解释——ω


### 波的振动性质

电磁波与机械波的性质差异:波速v求解的差异
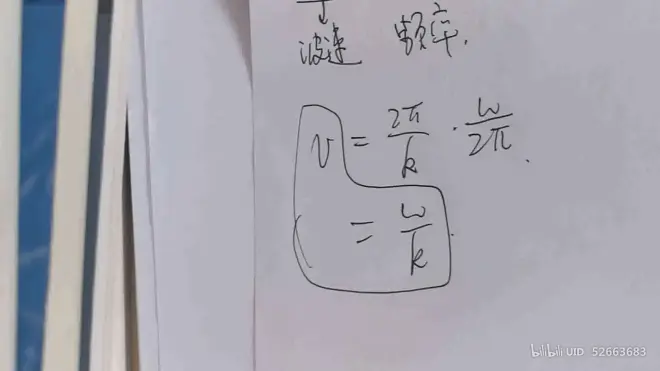
#### 波速v 的电磁学中的概述
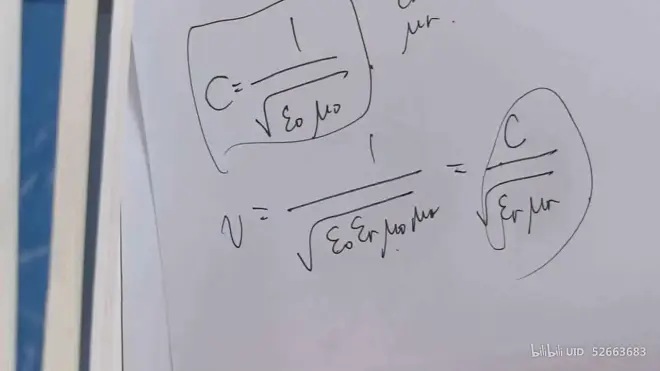

折射率n 的近似取值的原因
电磁波当中磁场是比较弱的,由公式E = vB_m,其中速度v 比较,致使E与B差了较大的数量级。此时磁场效应(磁化的相对磁导率μ_r)相比于电场效应(极化的相对介电常数ε_r)小

(电磁学:09麦克斯韦电磁理论-平面波)[https://www.bilibili.com/video/BV1ix411q74g/?p=2&;t=97]
- 波速的公式

### 光学研究的物理量
- 圆频率ω
- 频率ν(/nu/)
- 波长λ
- 波速v
- 折射率n

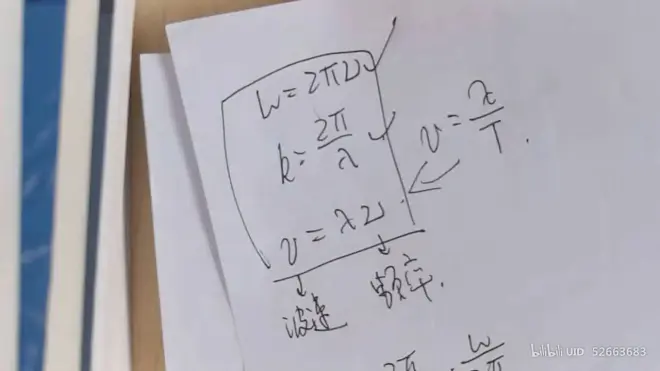
推论(光速c与折射率n)


### 波长λ
波长并不决定物体的颜色,如光通过不同介质时,颜色不变
#### 通过不同介质的波长性质
光通过不同介质的频率v不变

在同一种介质而言,物体的颜色由波长决定,而不同介质就不是。就本质而言,物体的颜色由光的频率v决定
电磁波谱
不同波长的波的名称

光谱
利用光现象研究物质或能量关系

图像:光强I-波长λ

自然光的光强I-波长λ图像

## 光的分类
- 单色光:由单一一种频率的光,自然条件下不存在完全的单色光
- 复色光: 由各种各样的单色光组合而成的光
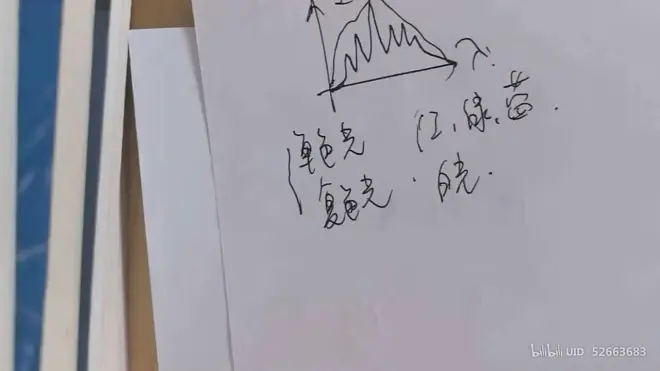
### 单色性
在光强I-波长λ图像的峰值之差衡量单色性

## 光强
- 能量密度:电磁场中单位体积内的储存能量
- 能流密度:电磁场中单位时间内能量在单位体积内的通过量
区别能流密度与能量密度

### 能量密度
讨论光的强度即为讨论能流密度,能流密度为坡印亭矢量S表达式=E× H

磁场强度H可表示为

可得坡印廷矢量S

注意:坡印廷矢量S、能量E、磁场强度H均为瞬时值
### 光强的定义
光强 I :平均光强


注意:以上是在正弦平面波之下才成立的
#### 光强处理的一些缺点
光强 I 与 E^2成正比
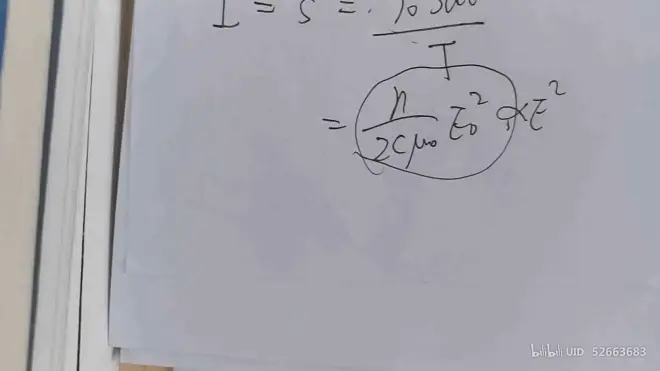
例如:

#### 光谱图象

当光为连续分布时,使用概率密度图像
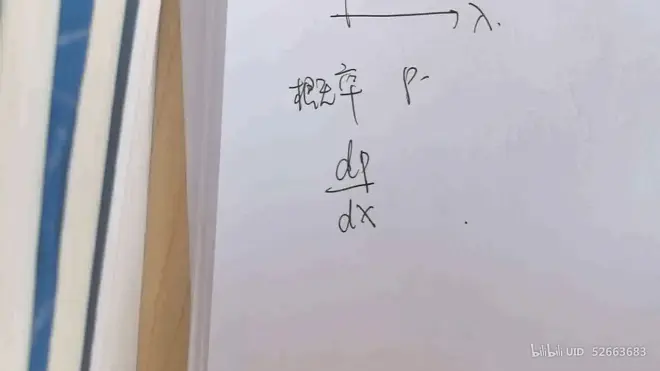

# 章节结语


近似问题
几何光学三大定律

# 几何光学
几何光学的成立条件:
- 介质均匀、各向同性
- 光强不太大
- 元件尺度远大于波长
# 几何光学三大定律
- 光的直线传播
- 反射定律
- 折射定律
## 光的直线传播
光在均匀介质中时沿着直线传播的
## 反射定律

## 折射定律
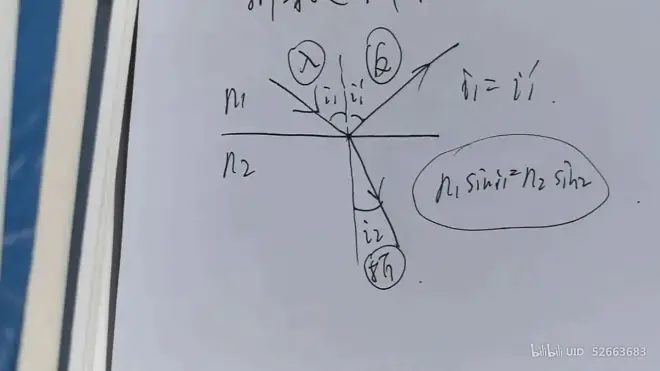
### 解释折射定律
原因:波矢k在界面的水平方向上连续


### 深度剖析反射与折射定律
#### 折射率n的判断


负折射率n
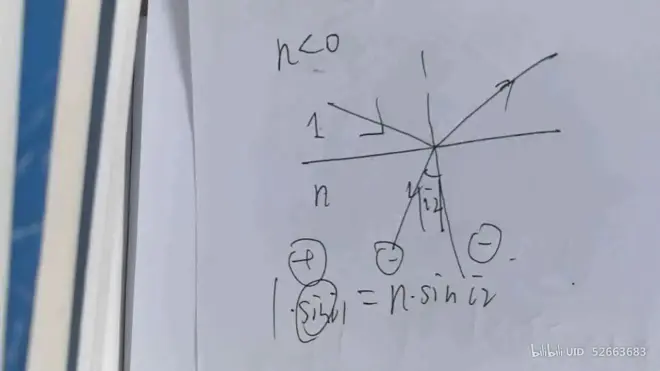
#### 全反射问题
条件:从光密介质到光疏介质

临界角θ_c
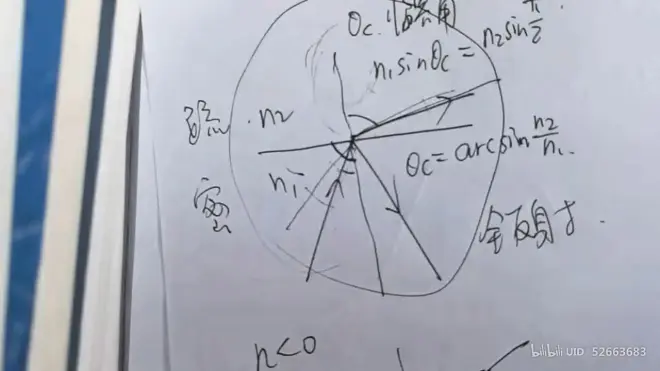
# 经典模型
## 平行玻璃板
- 证明:经过平行玻璃板的光为平行光

同时可以注意到

可得

- 求解平行平移距离x(已知入射角i_1很小)

证明:

由几何关系可得

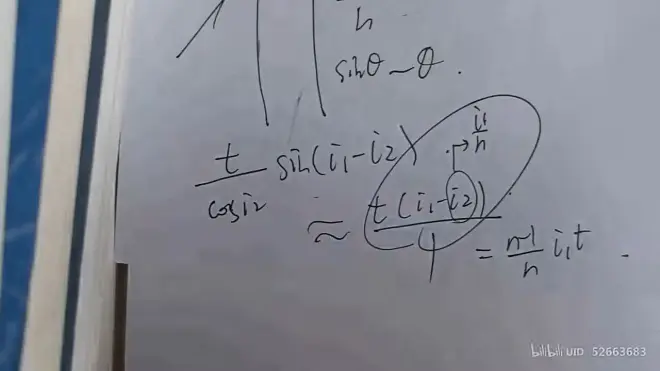
或者使用方法二,可得
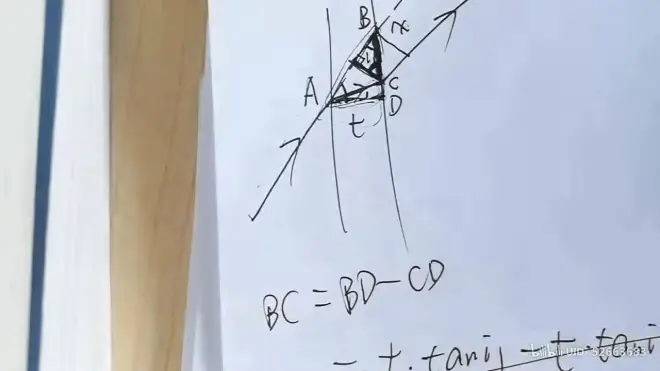

## 光楔
楔形:顶角非常小的三角形
求证:偏转角δ=(n-1)α

即为证明:
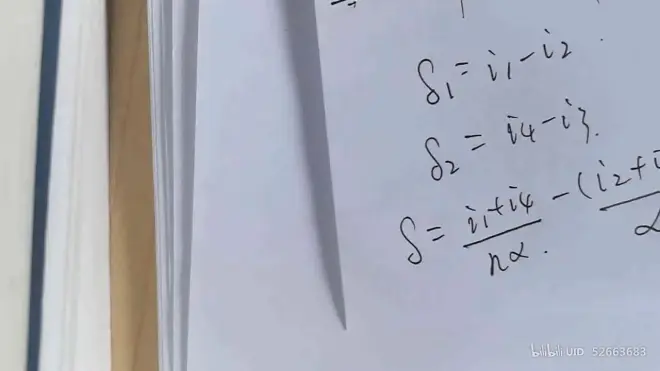
可知


## 多介质问题
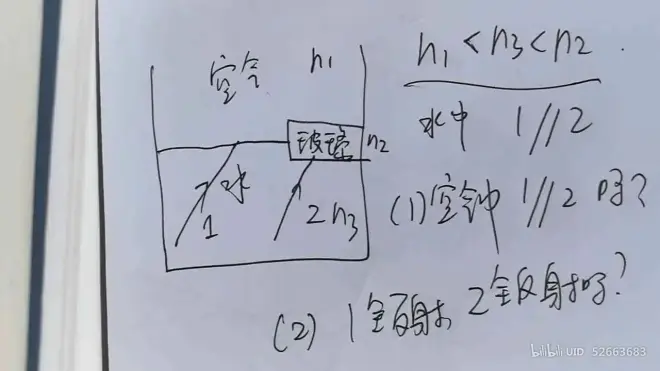

- 空气1//2

平行
- 1发生全反射,2也会发生全反射

# 章节结语
*棱镜、色散与连续折射

# 色散
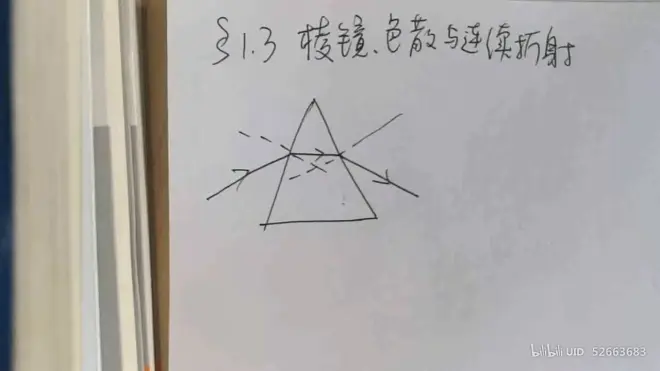
## 棱镜的折射问题
### 最小偏向角δ问题
已知三棱镜的顶角为α

假设:入射角 i1、出射角 i2、入射角 i3、出射角 i4
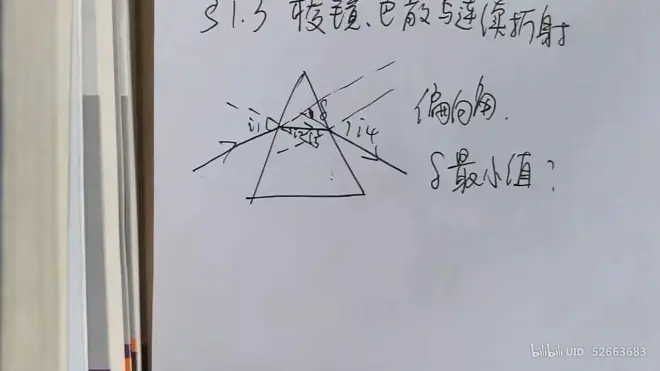
分析偏向角δ
结合绪论的四点共圆性质【https://www.bilibili.com/video/BV1mx41137dQ/?p=2&;t=136】,可得出以下分析结果

#### 求解最小偏向角——方法二
- 偏向角δ表达式求偏微分(非严谨分析)

可得

求出i1与i4的关系



同理可得

由 di2+di3 = 0 与 di1 = - di4 可得

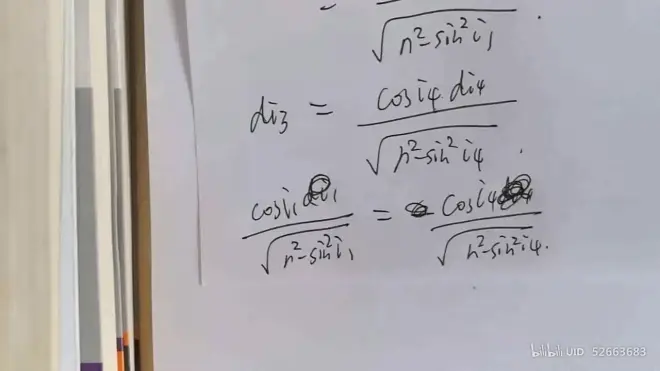
研究入射角 i1 与 出射角 i4 关系函数的基本性质(单调性、奇偶性、周期性...)
- 单调性判定


可知该函数为单调递减函数,即可得
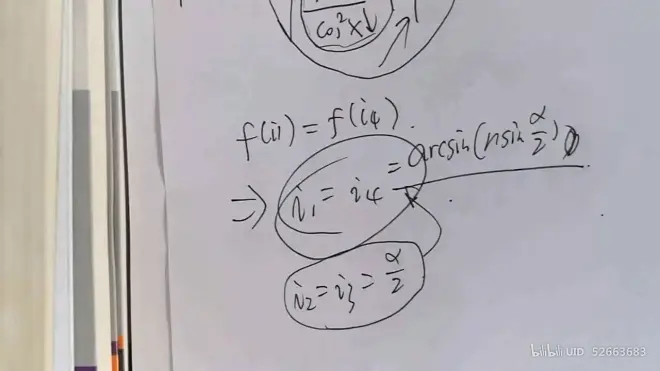
- i1与 i4的偏微分求解的探讨(严谨分析)
需求d^2 δ / d i^2_1 > 0 才可证明其为极小值

入射角 i1 与 出射角 i4 关系函数
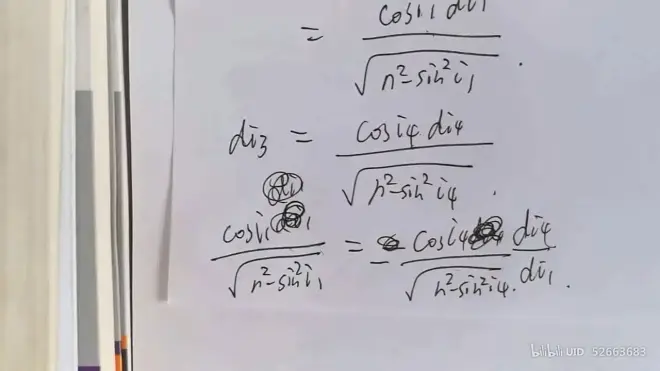
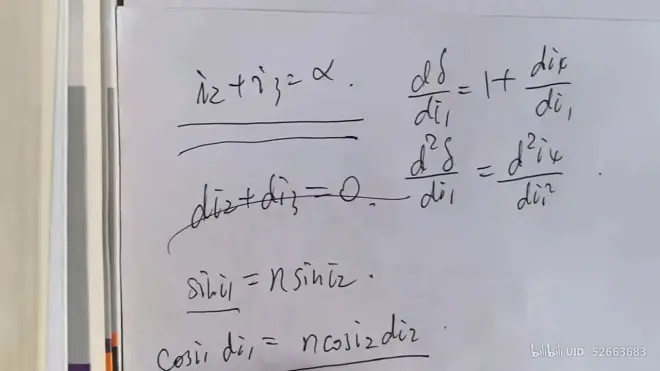
由于时间关系在此略写过程
#### 求解最小偏向角——方法二
追迹作图法
个人理解即为寻找一个满足光路关系的图以便直观研究偏转角δ与顶角α 、入射角 i1 、出射角 i4 的关系
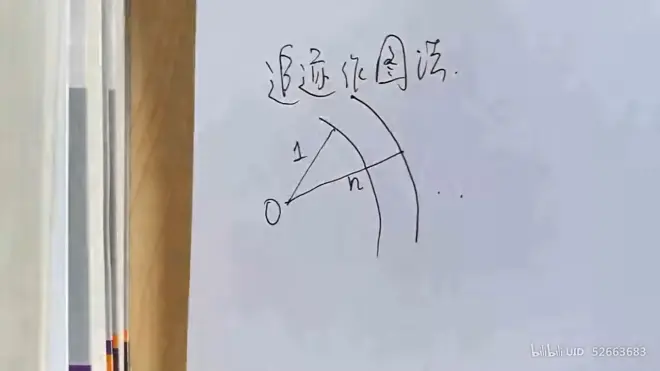


追迹作图法求解
求解偏向角δ最小 => 求解弦长PR最小


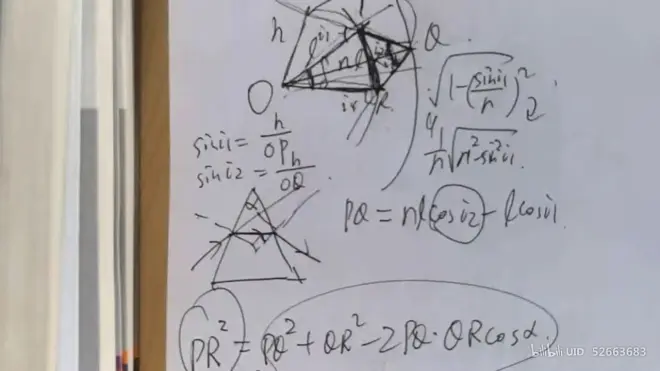
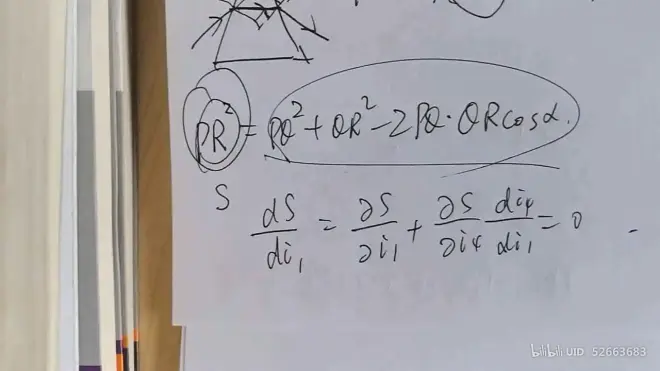
#### 棱镜最小偏向角性质的应用

当为以下状况时

可得求解折射率n的公式
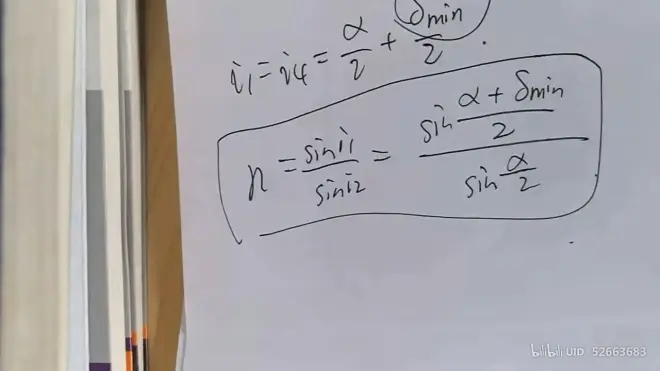
### 棱镜的偏向问题小结
## 色散问题
### 三棱镜的色散

由波长λ与折射率n的关系可得出

### 水滴的色散
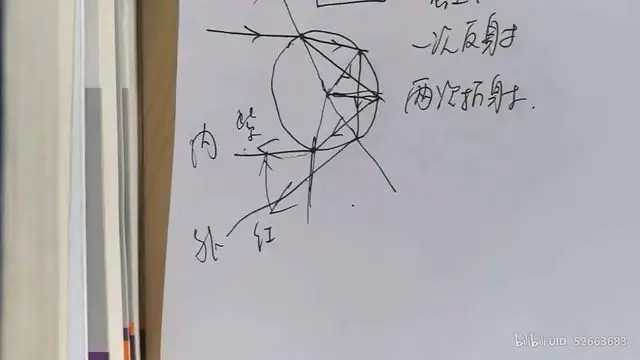
紫光偏向角度最大,红光偏向角度最小

## 折射率变化的光路
### 折射率n= f(Z)

设折射率函数为

且此时一束光线掠入射
#### 微元分析
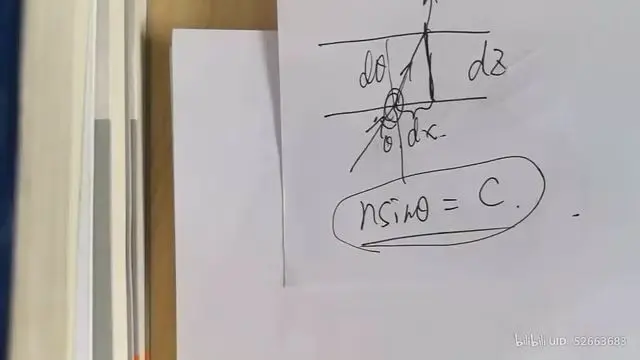
这里需要对cotθ的几何意义解释
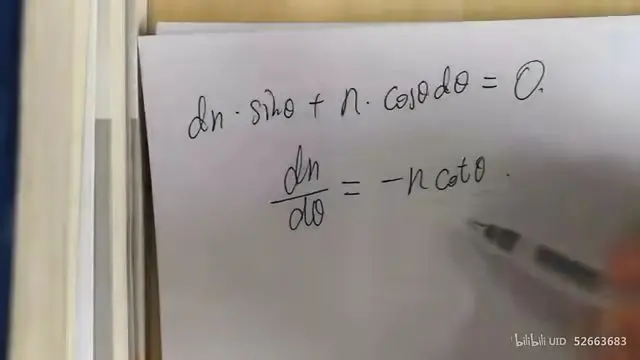

由此可得
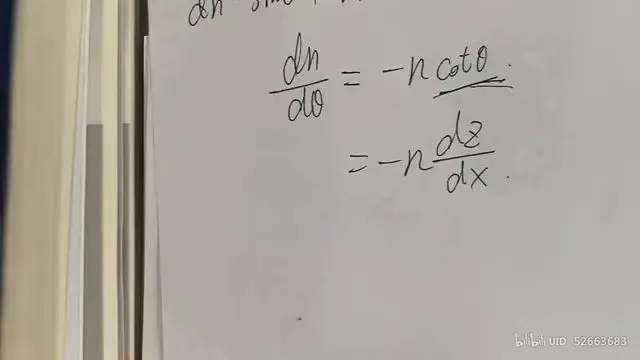

求出dθ/dx的关系式
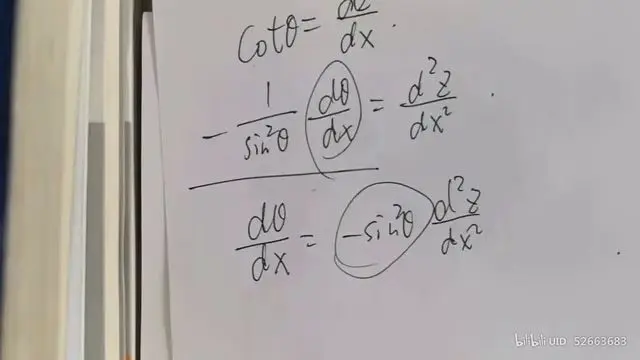
求出sin^2 θ
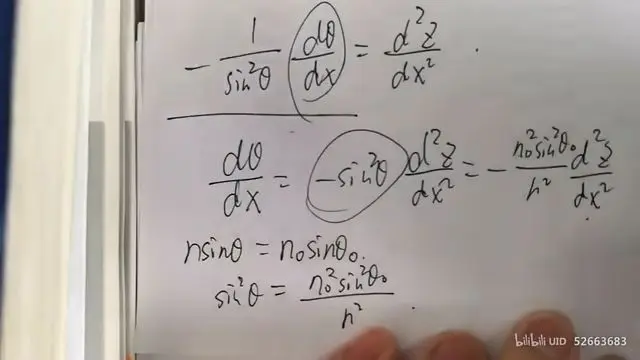
最终可得

亦可转化成以下结果

整理可得

#### 方程的求解问题


- 求解示例





更正

一些基础函数与推导

惠更斯原理与费马原理
# 惠更斯原理
## 现象
- 等相面
- 波面
- 波前

## 惠更斯内容的表述
在波面上的每一个点可视为后续波的波源

- 包络面
### 反射与折射

作包络线的垂线即为反射波

#### 反射定律的求解


#### 折射定律的求解

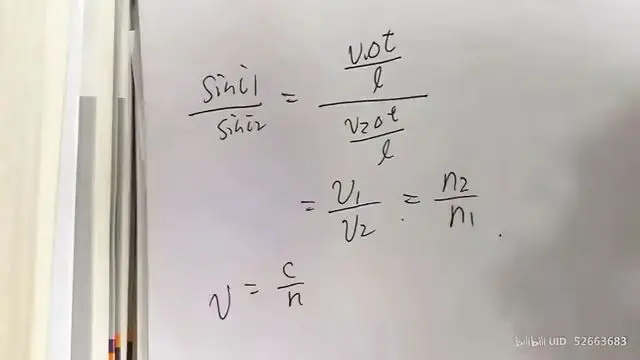
可证

#### 干涉与衍射
波动光学

惠更斯原理的一些缺陷
- 无法解释干涉为在光线不出现在后面的问题
# 费马原理
光在行进中选择最近的路径
- 不同介质当中


- 相同介质

## 费马原理的拓展
光程取驻点值点

## 费曼原理的数学形式

## 费曼原理的例子
- 直线
- 反射

- 折射


注意到
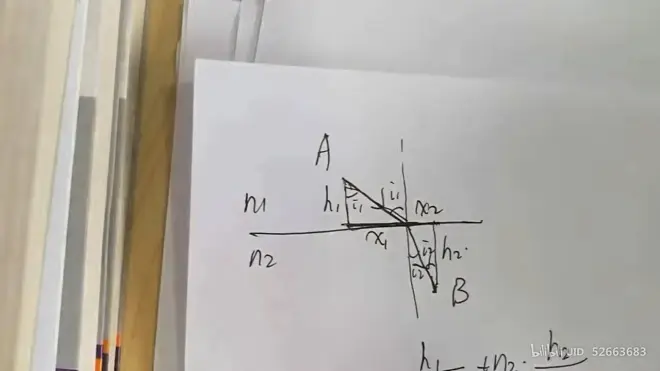
可得

整理可得
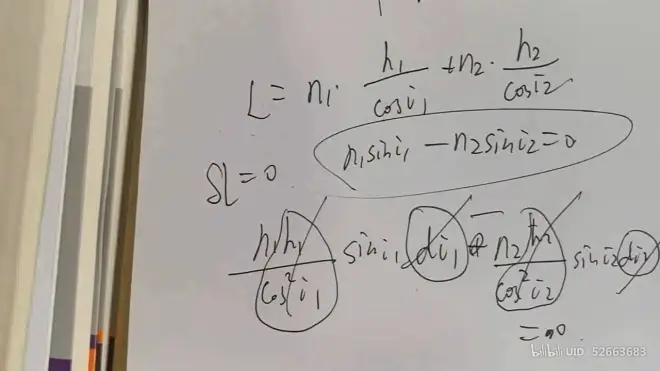
一些注意点
# 章节小结

